首页 > 数学 > 高考题 > 2023 > 2023年全国甲文

2023年高考数学甲卷-文10

2023年高考数学甲卷-文9<-->2023年高考数学甲卷-文11

（5分）在三棱锥

$P-ABC$ 中，

$\Delta ABC$ 是边长为2的等边三角形，

$PA=PB=2$ ，

$PC=\sqrt{6}$ ，则该棱锥的体积为

$($ 　　

$)$
A．1 B．

$\sqrt{3}$ C．2 D．3
答案：

$A$
分析：取

$AB$ 的中点

$D$ ，连接

$PD$ 、

$CD$ ，可得

$AB\bot$ 平面

$PCD$ ，再求出

$\Delta PCD$ 面积，然后利用棱锥体积公式求解．
解：如图，

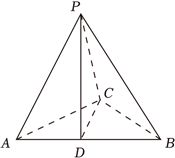
$PA=PB=2$ ，

$AB=BC=2$ ，取

$AB$ 的中点

$D$ ，连接

$PD$ ，

$CD$ ，
可得

$AB\bot PD$ ，

$AB\bot CD$ ，
又

$PD\bigcap CD=D$ ，

$PD$ 、

$CD\subset$ 平面

$PCD$ ，

$\therefore AB\bot$ 平面

$PCD$ ，
在

$\Delta PAB$ 与

$\Delta ABC$ 中，求得

$PD=CD=\sqrt{{2}^{2}-{1}^{2}}=\sqrt{3}$ ，
在

$\Delta PCD$ 中，由

$PD=CD=\sqrt{3}$ ，

$PC=\sqrt{6}$ ，得

$PD^{2}+CD^{2}=PC^{2}$ ，则

$PD\bot CD$ ，

$\therefore$

${S}_{\Delta PCD}=\dfrac{1}{2}\times PD\times CD=\dfrac{1}{2}\times \sqrt{3}\times \sqrt{3}=\dfrac{3}{2}$ ，

$\therefore$

${V}_{P-ABC}=\dfrac{1}{3}{S}_{\Delta PCD}\times AB=\dfrac{1}{3}\times \dfrac{3}{2}\times 2=1$ ．
故选：

$A$ ．
点评：本题考查多面体体积的求法，训练了利用等积法求多面体的体积，是中档题．

2023年高考数学甲卷-文9<-->2023年高考数学甲卷-文11

全网搜索"2023年高考数学甲卷-文10"相关

相关知识

无相关信息

学习笔记（共有 0 条）