|
2022年高考数学乙卷-理10<-->2022年高考数学乙卷-理12
(5分)双曲线$C$的两个焦点为$F_{1}$,$F_{2}$,以$C$的实轴为直径的圆记为$D$,过$F_{1}$作$D$的切线与$C$交于$M$,$N$两点,且$\cos \angle F_{1}NF_{2}=\dfrac{3}{5}$,则$C$的离心率为( )
A.$\dfrac{\sqrt{5}}{2}$ B.$\dfrac{3}{2}$ C.$\dfrac{\sqrt{13}}{2}$ D.$\dfrac{\sqrt{17}}{2}$
分析:当直线与双曲线交于两支时,设双曲线的方程为$\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1(a > 0,b > 0)$,设过$F_{1}$的切线与圆$D:x^{2}+y^{2}=a^{2}$相切于点$P$,从而可求得$\vert PF_{1}\vert$,过点$F_{2}$作$F_{2}Q\bot MN$于点$Q$,由中位线的性质可求得$\vert F_{1}Q\vert$,$\vert QF_{2}\vert$,在$\rm{Rt}\Delta QNF_{2}$中,可求得$\vert NF_{2}\vert$,$\vert NQ\vert$,利用双曲线的定义可得$a$,$b$的关系,再由离心率公式求解即可.情况二当直线与双曲线交于一支时,同理可求得离心率.
解:当直线与双曲线交于两支时,设双曲线的方程为$\dfrac{{x}^{2}}{{a}^{2}}-\dfrac{{y}^{2}}{{b}^{2}}=1(a > 0,b > 0)$,

设过$F_{1}$的切线与圆$D:x^{2}+y^{2}=a^{2}$相切于点$P$,
则$\vert OP\vert =a$,$OP\bot PF_{1}$,又$\vert OF_{1}\vert =c$,
所以$PF_{1}=\sqrt{O{{F}_{1}}^{2}-O{P}^{2}}=\sqrt{{c}^{2}-{a}^{2}}=b$,
过点$F_{2}$作$F_{2}Q\bot MN$于点$Q$,
所以$OP//F_{2}Q$,又$O$为$F_{1}F_{2}$的中点,
所以$\vert F_{1}Q\vert =2\vert PF_{1}\vert =2b$,$\vert QF_{2}\vert =2\vert OP\vert =2a$,
因为$\cos \angle F_{1}NF_{2}=\dfrac{3}{5}$,$\angle F_{1}NF_{2} < \dfrac{\pi }{2}$,所以$\sin \angle F_{1}NF_{2}=\dfrac{4}{5}$,
所以$\vert NF_{2}\vert =\dfrac{Q{F}_{2}}{\sin \angle {F}_{1}N{F}_{2}}=\dfrac{5a}{2}$,则$\vert NQ\vert =\vert NF_{2}\vert \cdot \cos \angle F_{1}NF_{2}=\dfrac{3a}{2}$,
所以$\vert NF_{1}\vert =\vert NQ\vert +\vert F_{1}Q\vert =\dfrac{3a}{2}+2b$,
由双曲线的定义可知$\vert NF_{1}\vert -\vert NF_{2}\vert =2a$,
所以$\dfrac{3a}{2}+2b-\dfrac{5a}{2}=2a$,可得$2b=3a$,即$\dfrac{b}{a}=\dfrac{3}{2}$,
所以$C$的离心率$e=\dfrac{c}{a}=\sqrt{1+\dfrac{{b}^{2}}{{a}^{2}}}=\sqrt{1+\dfrac{9}{4}}=\dfrac{\sqrt{13}}{2}$.
情况二:当直线与双曲线交于一支时,
如图,记切点为$A$,连接$OA$,则$\vert OA\vert =a$,$\vert F_{1}A\vert =b$,
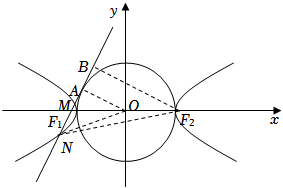
过$F_{2}$作$F_{2}B\bot MN$于$B$,则$\vert F_{2}B\vert =2a$,因为$\cos \angle F_{1}NF_{2}=\dfrac{3}{5}$,所以$\vert NF_{2}\vert =\dfrac{5a}{2}$,$\vert NB\vert =\dfrac{3a}{2}$,
$\vert NF_{2}\vert -\vert NF_{1}\vert =\dfrac{5a}{2}-(\dfrac{3a}{2}-2b)=a+2b=2a$,即$a=2b$,
所以$e=\dfrac{c}{a}=\sqrt{1+\dfrac{{b}^{2}}{{a}^{2}}}=\sqrt{1+\dfrac{1}{4}}=\dfrac{\sqrt{5}}{2}$,$A$正确.
故选:$AC$.
点评:本题主要考查双曲线的性质,圆的性质,考查转化思想与数形结合思想,考查运算求解能力,属于中档题.
2022年高考数学乙卷-理10<-->2022年高考数学乙卷-理12
全网搜索"2022年高考数学乙卷-理11"相关
|

