|
2022年高考数学北京13<-->2022年高考数学北京15
(5分)设函数$f(x)=\left\{\begin{array}{l}{-ax+1,x < a,}\\ {{{(x-2)}^2},x\geqslant a\cdot }\end{array}\right.$若$f(x)$存在最小值,则$a$的一个取值为 0 ;$a$的最大值为 .
分析:对函数$f(x)$分段函数的分界点进行分类讨论,研究其不同图像时函数取最小值时$a$的范围即可.
解答:解:当$a < 0$时,函数$f(x)$图像如图所示,不满足题意,

当$a=0$时,函数$f(x)$图像如图所示,满足题意;
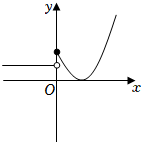
当$0 < a < 2$时,函数$f(x)$图像如图所示,要使得函数有最小值,需满足$-a^{2}+1\geqslant 0$,解得:$0 < a\leqslant 1$;
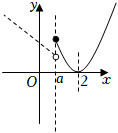
当$a=2$时,函数$f(x)$图像如图所示,不满足题意,
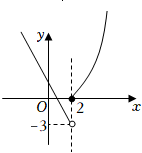
当$a > 2$时,函数$f(x)$图像如图所示,要使得函数$f(x)$有最小值,需$(a-2)^{2}\leqslant -a^{2}+1$,无解,故不满足题意;
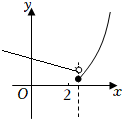
综上所述:$a$的取值范围是$[0$,$1]$,
故答案为:0,1.
点评:本题主要考查利用分段函数图像确定函数最小值是分界点的讨论,属于较难题目.
2022年高考数学北京13<-->2022年高考数学北京15
全网搜索"2022年高考数学北京14"相关
|

