|
2021年高考数学浙江20<-->2021年高考数学浙江22
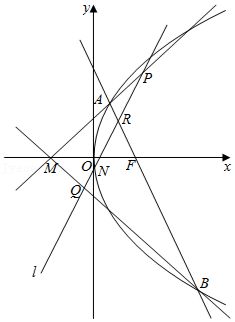
21.(15分)如图,已知$F$是抛物线$y^{2}=2px(p>0)$的焦点,$M$是抛物线的准线与$x$轴的交点,且$\vert MF\vert =2$.
(Ⅰ)求抛物线的方程:
(Ⅱ)设过点$F$的直线交抛物线于$A$,$B$两点,若斜率为2的直线$l$与直线$MA$,$MB$,$AB$,$x$轴依次交于点$P$,$Q$,$R$,$N$,且满足$\vert RN\vert ^{2}=\vert PN\vert \cdot \vert QN\vert$,求直线$l$在$x$轴上截距的取值范围.
分析:(Ⅰ)根据题意求得$p$,进而求得抛物线方程;
(Ⅱ)设直线$AB:y=k(x-1)$,与抛物线方程联立,利用韦达定理求得两根之和及两根之积,设直线$AM$及直线$BM$方程,将它们分别与直线$l$方程$y=2(x-t)$联立,可得点$R$及点$Q$的横坐标,再根据题意,可得$(\dfrac{k-kt}{k-2})^{2}=\dfrac{{k}^{2}(1+t)^{2}}{3{k}^{2}+4}$,化简将含$t$的式子用$k$表示,进而得到关于$t$的不等式,解出即可.
解:(Ⅰ)依题意,$p=2$,故抛物线的方程为$y^{2}=4x$;
(Ⅱ)由题意得,直线$AB$的斜率存在且不为零,设直线$AB:y=k(x-1)$,
将直线$AB$方程代入抛物线方程可得,$k^{2}x^{2}-(2k^{2}+4)x+k^{2}=0$,
则由韦达定理有,${x}_{A}+{x}_{B}=2+\dfrac{4}{{k}^{2}},{x}_{A}{x}_{B}=1$,则$y_{A}y_{B}=-4$,
设直线$AM:y=k_{1}(x+1)$,其中${k}_{1}=\dfrac{{y}_{A}}{{x}_{A}+1}$,设直线$BM:y=k_{2}(x+1)$,其中${k}_{2}=\dfrac{{y}_{B}}{{x}_{B}+1}$,
则${k}_{1}+{k}_{2}=\dfrac{{y}_{A}}{{x}_{A}+1}+\dfrac{{y}_{B}}{{x}_{B}+1}=\dfrac{{y}_{A}{x}_{B}+{y}_{A}+{y}_{B}{x}_{A}+{y}_{B}}{({x}_{A}+1)({x}_{B}+1)}=\dfrac{k({x}_{A}-1){x}_{B}+k({x}_{A}-1)+k({x}_{B}-1){x}_{A}+k({x}_{B}-1)}{({x}_{A}+1)({x}_{B}+1)}=\dfrac{0}{({x}_{A}+1)({x}_{B}+1)}=0$,
${k}_{1}{k}_{2}=\dfrac{{y}_{A}{y}_{B}}{({x}_{A}+1)({x}_{B}+1)}=\dfrac{-4}{1+2+\dfrac{4}{{k}^{2}}+1}=\dfrac{-{k}^{2}}{1+{k}^{2}}$,
设直线$l:y=2(x-t)$,
联立$\left\{\begin{array}{l}{y=2(x-t)}\\ {y=k(x-1)}\end{array}\right.$,可得${x}_{R}=\dfrac{k-2t}{k-2}$,则$\vert {x}_{R}-t\vert =\vert \dfrac{k-2t}{k-2}-t\vert =\vert \dfrac{k-kt}{k-2}\vert$,
联立$\left\{\begin{array}{l}{y=2(x-t)}\\ {y={k}_{1}(x+1)}\end{array}\right.$,可得${x}_{P}=\dfrac{{k}_{1}+2t}{2-{k}_{1}}$,则$\vert {x}_{P}-t\vert =\vert \dfrac{{k}_{1}+2t}{2-{k}_{1}}-t\vert =\vert \dfrac{{k}_{1}+{k}_{1}t}{2-{k}_{1}}\vert$,
同理可得,${x}_{Q}=\dfrac{{k}_{2}+2t}{2-{k}_{2}},\vert {x}_{Q}-t\vert =\vert \dfrac{{k}_{2}+{k}_{2}t}{2-{k}_{2}}\vert$,
又$\vert RN\vert ^{2}=\vert PN\vert \cdot \vert QN\vert$,
$\therefore$$\vert \dfrac{k-kt}{k-2}{\vert }^{2}=\vert \dfrac{{k}_{1}+{k}_{1}t}{2-{k}_{1}}\cdot \dfrac{{k}_{2}+{k}_{2}t}{2-{k}_{2}}\vert$,即$(\dfrac{k-kt}{k-2})^{2}=\dfrac{{k}^{2}(1+t)^{2}}{3{k}^{2}+4}$,
$\therefore$$\dfrac{(1+t)^{2}}{(t-1)^{2}}=\dfrac{3{k}^{2}+4}{(k-2)^{2}}=\dfrac{3(k-2)^{2}+12(k-2)+16}{(k-2)^{2}}=\dfrac{16}{(k-2)^{2}}+\dfrac{12}{k-2}+3=(\dfrac{4}{k-2}+\dfrac{3}{2})^{2}+\dfrac{3}{4}\geqslant \dfrac{3}{4}(t\ne 1)$,
$\therefore 4(t^{2}+2t+1)\geqslant 3(t^{2}-2t+1)$,即$t^{2}+14t+1\geqslant 0$,解得$t\geqslant 4\sqrt{3}-7$或$t\leqslant -7-4\sqrt{3}(t\ne 1)$;
当直线$AB$的斜率不存在时,则直线$AB:x=1$,$A(1,2)$,$B(1,-2)$,$M(-1,0)$,
$\therefore$直线$MA$的方程为$y=x+1$,直线$MB$的方程为$y=-x-1$,
设直线$l:y=2(x-t)$,则$P(1+2t,2+2t)$,$Q(\dfrac{2t-1}{3},-\dfrac{2t+2}{3})$,$R(1,2-2t)$,$N(t,0)$,
又$\vert RN\vert ^{2}=\vert PN\vert \cdot \vert QN\vert$,故$(1-t)^{2}+(2-2t)^{2}=\sqrt{(1+t)^{2}+(2+2t)^{2}}\cdot \sqrt{(\dfrac{2t-1}{3}-t)^{2}+(-\dfrac{2t+2}{3})^{2}}$,
解得$t$满足$(-\infty ,-7-4\sqrt{3}]\bigcup{[}4\sqrt{3}-7,1)\bigcup (1,+\infty )$.
$\therefore$直线$l$在$x$轴上截距的取值范围为$(-\infty ,-7-4\sqrt{3}]\bigcup{[}4\sqrt{3}-7,1)\bigcup (1,+\infty )$.
点评:本题考查抛物线方程的求法,考查直线与抛物线的位置关系,考查运算求解能力,属于难题.
2021年高考数学浙江20<-->2021年高考数学浙江22
全网搜索"2021年高考数学浙江21"相关
|

