|
2021年高考数学浙江6<-->2021年高考数学浙江8
7.(4分)已知函数$f(x)=x^{2}+\dfrac{1}{4}$,$g(x)=\sin x$,则图象为如图的函数可能是( )
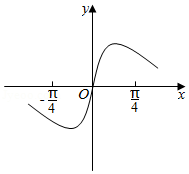
A.$y=f(x)+g(x)-\dfrac{1}{4}$ B.$y=f(x)-g(x)-\dfrac{1}{4}$
C.$y=f(x)g(x)$ D.$y=\dfrac{g(x)}{f(x)}$
分析:可以判断所求函数为奇函数,利用函数的奇偶性可排除选项$A$,$B$;利用函数在$(0,\dfrac{\pi }{4})$上的单调性可判断选项$C$,$D$.
解:由图可知,图象关于原点对称,则所求函数为奇函数,
因为$f(x)=x^{2}+\dfrac{1}{4}$为偶函数,$g(x)=\sin x$为奇函数,
函数$y=f(x)+g(x)-\dfrac{1}{4}=x^{2}+\sin x$为非奇非偶函数,故选项$A$错误;
函数$y=f(x)-g(x)-\dfrac{1}{4}=x^{2}-\sin x$为非奇非偶函数,故选项$B$错误;
函数$y=f(x)g(x)=(x^{2}+\dfrac{1}{4})\sin x$,则$y'=2x\sin x+(x^{2}+\dfrac{1}{4})\cos x>0$对$x\in (0,\dfrac{\pi }{4})$恒成立,
则函数$y=f(x)g(x)$在$(0,\dfrac{\pi }{4})$上单调递增,故选项$C$错误.
故选:$D$.
点评:本题考查了函数图象的识别,解题的关键是掌握识别图象的方法:可以从定义域、值域、函数值的正负、特殊点、特殊值、函数的性质等方面进行判断,考查了直观想象能力与逻辑推理能力,属于中档题.
2021年高考数学浙江6<-->2021年高考数学浙江8
全网搜索"2021年高考数学浙江7"相关
|

