福建(理)
一、选择题(每小题5分)
(3)已知![]() 则
则![]() 等于()
等于()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
浙江(理)
一、选择题(每小题5分)
(6)函数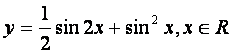 的值域是()
的值域是()
(A)[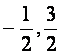 ] (B)[
] (B)[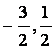 ]
]
(C)[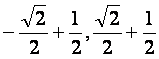 ] (D)[
] (D)[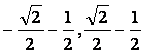 ]
]
三、解答题
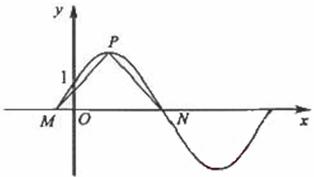
(15)如图,函数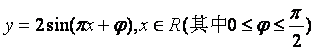 的图象与y轴交于点(0,1)
的图象与y轴交于点(0,1)
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求![]() 与
与![]() 的夹角。
的夹角。
天津(理)
一、选择题(每小题5分)
(8)已知函数f(x)=asinx-bcosx(a、b为常数,a≠0,x∈R)在x=![]() 处取得最
处取得最
小值,则函数y=f(![]() -x)是(D)
-x)是(D)
(A)偶函数且它的图象关于点(π,0)对称 (B)偶函数且它的图象关于点(![]() ,0)对称
,0)对称
(C)奇函数且它的图象关于点(![]() ,0)对称
(D)奇函数且它的图象关于点(π,0)对称
,0)对称
(D)奇函数且它的图象关于点(π,0)对称
三、解答题
(17)(本小题满分12分)
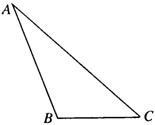
如图,在△ABC中,AC=2,BC=l,cosC=![]() .
.
(Ⅰ)求AB的值;
(Ⅱ)求sin(2A+C)的值.
江苏
一、选择题(每小题5分)
(1)已知![]() ,函数
,函数![]() 为奇函数,则a=()
为奇函数,则a=()
(A)0 (B)1 (C)-1 (D)±1
(4)为了得到函数![]() 的图像,只需把函数
的图像,只需把函数![]() 的图像上所有的点()
的图像上所有的点()
(A)向左平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的![]() 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
二、填空题(每小题5分)
(14)![]() =
=
辽宁(理)
一、选择题(每小题5分)
(11)已知函数![]() ,则
,则![]() 的值域是()
的值域是()
(A)![]() (B)
(B)
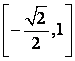 (C)
(C)
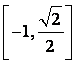 (D)
(D)
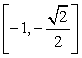
二、填空题(每小题4分)
(16)
若一条直线与一个正四棱柱各个面所成的角都为![]() ,则
,则![]() =______
=______
三. 解答题
(17) (本小题满分12分)
已知函数![]() ,
,![]() .求:
.求:
(I)
函数![]() 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量![]() 的集合;
的集合;
(II)
函数![]() 的单调增区间.
的单调增区间.
重庆(理)
一、填空题(每题4分)
(13)已知![]() ,
,![]() ,
,![]() ,则
,则![]() 。
。
三、解答题
(17)(本小题满分13分)
设函数![]() (其中
(其中![]() )。且
)。且![]() 的图像在
的图像在![]() 轴右侧的第一个
轴右侧的第一个
最高点的横坐标是![]() 。
。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)如果![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的值;
的值;
湖南(理)
二、填空题(每小题4分)
14.若f(x)=asin(x+![]() )+bsin(x-
)+bsin(x-![]() )(ab≠0)是偶函数,则有序实数对(a,b)
)(ab≠0)是偶函数,则有序实数对(a,b)
可以是 .(注:只要填满足a+b=0的一组数字即可)(写出你认为正
确的一组数字即可).
三、解答题
16.(本小题满分12分)
如图3,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ABC=β.
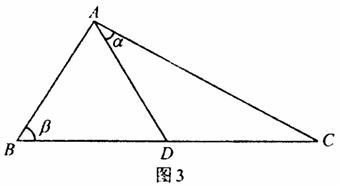
(Ⅰ)证明:sinα+cos2β=0;
(Ⅱ)若AC=![]() DC,求β的值.
DC,求β的值.
湖北(理)
一、选择题(每小题5分)
3.若△ABC的内角A满足sin2A=![]() ,则sinA+cosA=
()
,则sinA+cosA=
()
A.![]() B.
B.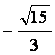 C.
C.![]() D.
D.![]()
三、解答题
16.(本小题满分12分)
设函数![]() ·(b+c),其中向量a=(sinx,—cosx),b=(sinx,—3cosx),
·(b+c),其中向量a=(sinx,—cosx),b=(sinx,—3cosx),
c=(—cosx,sinx),x![]() 。
。
(Ⅰ)求函数f(x)的最大值和最小正周期;
(Ⅱ)将函数y=f(x)的图像按向量d平移,使平移后得到的图象关于坐标
原点成中心对称,求长度最小的d。
广东
一、选择题(每题5分)
3.下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、解答题
15.(本小题满分14分)
已知函数![]()
(Ⅰ)求f(x)的最小正周期:![]()
(Ⅱ)求f(x)的最大值和最小值:
(Ⅲ)若![]() 求sin2
求sin2![]() 的值。
的值。
北京(理)
二、填空题(每小题5分)
(12)在△ABC中,若sinA:sin B:sinC=5:7:8,则∠B的大小是____.解答
三、解答题
(15)(本小题共12分)
已知函数f(x)=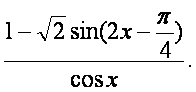
(Ⅰ)求f(x)的定义域;
(Ⅱ)设α是第四象限的角,且tanα=-![]() 求f(α)的值.
求f(α)的值.
上海(理)
一、填空题(每小题4分)
6.如果![]() =
=![]() ,且
,且![]() 是第四象限的角,那么
是第四象限的角,那么![]() =
.
=
.
三、解答题
17.(本题满分12分)
求函数![]() =2
=2![]() +
+![]() 的值域和最小正周期.
的值域和最小正周期.
山东(理)
一、选择题(每小题5分)
4.在△ABC中,角A、B、C的对边分别为a、b、c,已知A=![]() ,a=
,a=![]() ,b=1,
,b=1,
则c=()
(A)1 (B)2 (C)![]() -1
(D)
-1
(D)![]()
三、解答题
17.(本小题满分12分)
已知函数F(x)=Asin2(ωx+φ)(A>0,ω>0,0<φ<![]() ),且y=f(x)的最大值为2,
),且y=f(x)的最大值为2,
其图象相邻两对称轴间的距离为2,并过点(1,2).
(Ⅰ)求φ;
(Ⅱ)计算f(1)+f(2)+…+f(2008).
江西(理)
一、选择题(每小题5分)
16.已知圆M:(x+cosθ)2+(y-sin θ)2=1,直线l:y=kx,下面四个命题
(A)对任意实数k和θ,直线l和圆M相切;
(B)对任意实数k和θ,直线l和圆M有公共点;
(C)对任意实数θ,必存在实数k,使得直线l和圆M相切;
(D)对任意实数k,必存在实数θ,使得直线l和圆M相切.
其中真命题的代号是_________(写出所有真命题的代号).
三、解答题
19.(本小题满分12分)
如图,已知△ABC是边长为1的正三角形,M、N分别是边AB、AC上的
点,线段MN经过△ABC的中心G.设∠MGA=α(![]() ≤α≤
≤α≤![]() ).
).
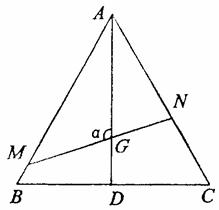
(1)试将△AGM、△AGN的面积(分别记为S1与S2)表示为α的函数;
(2)求y=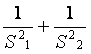 的最大值与最小值.
的最大值与最小值.
陕西(理)
一、选择题(每小题5分)
6.![]() 等式
等式![]() 成立
成立![]() 是
是![]()
![]() 成等差数列
成等差数列
![]() 的()
的()
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分又不必要条件
二、填空题(每小题4分)
13.![]() 的值为______。解答
的值为______。解答
三、解答题
(17)(本小题满分12分)
已知函数
(I)求函数![]() 的最小正周期;
的最小正周期;
(II)求使函数![]() 取得最大值的
取得最大值的![]() 集合。
集合。
安徽(理)
一、选择题(每小题5分)
(11)如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
(A)△A1B1C1和△A2B2C2都是锐角三角形
(B)△A1B1C1和△A2B2C2都是钝角三角形
(C)△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
(D)△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
三、解答题
(17)(本小题满分12分)
已知![]() <
<![]() <
<![]() ,tan
,tan![]() +cot
+cot![]() =
=![]() 。
。
(Ⅰ)求tan![]() 的值
的值
(Ⅱ)求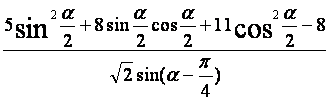 的值。
的值。
四川(理)
一、选择题(每小题5分)
(5)下列函数中,图象的一部分如图所示的是()
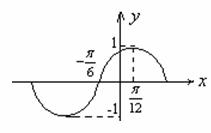
(A)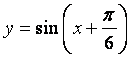 (B)
(B)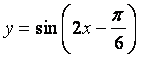
(C)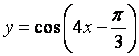 (D)
(D)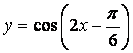
(11)设![]() 分别是
分别是![]() 的三个内角
的三个内角![]() 所对的边,则
所对的边,则![]()
是![]() 的()
的()
(A)充要条件 (B)充分而不必要条件
(C)必要而不充分条件 (D)既不充分又不必要条件
三、解答题
(17)(本大题满分12分)
已知![]() 是三角形
是三角形![]() 三内角,向量m=(-1,
三内角,向量m=(-1,![]() ),n=(cosA,sinA),且mn=1.
),n=(cosA,sinA),且mn=1.
(Ⅰ)求角![]() ;
;
(Ⅱ)若 ,求tanC.
,求tanC.
全国卷(Ⅰ)理
一、选择题(每小题5分)
(5)函数 的单调增区间为()
的单调增区间为()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)
(6)![]() 的内角A、B、C的对边分别为
的内角A、B、C的对边分别为![]() 若
若![]() 成等比数列,
成等比数列,
且c=2a,则cosB=()
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(16)设函数![]() .若
.若![]() 是奇函数,则
是奇函数,则![]() = 。
= 。
三.解答题
(17)(本小题满分12分)
![]() 的三个内角为A、B、C,求当A为何值时
的三个内角为A、B、C,求当A为何值时![]() 取得最大值,
取得最大值,
并求出这个最大值。
全国卷(Ⅱ)理
一、选择题(每小题5分)
(2)函数![]() 的最小正周期是(
)
的最小正周期是(
)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)若![]() 则
则![]()
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。