，α∈(
，
)，求cos2α和sin(2α+)的值.
（17）(本小题满分12分)
已知tanα+cotα=，α∈(，)，求cos2α和sin(2α+)的值.
本小题考查同角三角函数关系、两角和公式、倍角公式等基础知识，
考查基本运算能力.满分12分.
解法—：由tanα+cotα=
，得
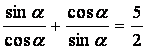，则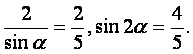
因为α∈(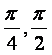
)，所以2α∈(
，π)，cos2α=-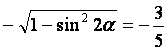
sin(2α+
)=sin2α·cos
+cos2α·sin
=
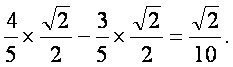
解法二:由tanα+cotα=，得
tanα+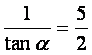
,
解得tanα=2或tanα=
.由已知α∈(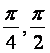
),故舍去tanα=
,得
tanα=2.
因此,sin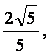α=
cosα=
,那么cos2α=cos2α-sin2α=-
,
且sin2α=2sinαcosα=
,故
sin(2α+
)=sin2α·cos+cos2α·sin
=
×
.
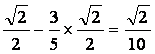本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。