|
定积分的概念<-->微积分基本定理
定积分的数学定义
定积分的数学定义:
设f(x)是在区间[a,b]上有定义的函数,在a,b之间取若干分点,
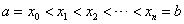 ,记小区间 ,记小区间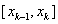 为 为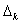 ,其长度为 ,其长度为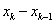 ,记作 ,记作 , , 中最大的记作d,再在每个小区间 中最大的记作d,再在每个小区间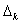 上任取一点代表点 上任取一点代表点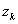 ,做和式: ,做和式:


如果(不论如何取 分点和代表点 分点和代表点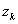 )当d趋于0时和式以S为极限,就说函数f(x)在上[a,b]可积,并且说S是f(x)在[a,b]的定积分,记作 )当d趋于0时和式以S为极限,就说函数f(x)在上[a,b]可积,并且说S是f(x)在[a,b]的定积分,记作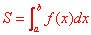 . .
“当d趋于0时和式以S为极限”,意思是“当d越来越小时,和式越来越接近于S,要多接近,就有多接近”。
定积分的几何意义:当函数f(x)在区间[a,b]上恒为正时,定积分 的几何意义是以曲线f(x)为曲边的曲边梯形面积。一般情况下,定积分 的几何意义是以曲线f(x)为曲边的曲边梯形面积。一般情况下,定积分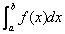 的几何意义是介于x轴、函数f(x)的图象以及直线 的几何意义是介于x轴、函数f(x)的图象以及直线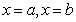 之间各部分面积的代数和,在x轴上方的面积取正号;在x轴下方的面积取负号。 之间各部分面积的代数和,在x轴上方的面积取正号;在x轴下方的面积取负号。
|

