|
求切线方程<-->直线与圆的方程的应用
圆与圆的位置关系
Ⅰ、两圆的位置关系:
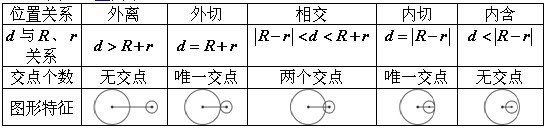

Ⅱ、判断方法:
⑴几何方法:
由两个圆的圆心坐标、半径长、连心线长的关系来判断。
1° 当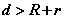 时,圆 时,圆 与圆 与圆 外离; 外离;
2° 当 时,圆 时,圆 与圆 与圆 外切; 外切;
3° 当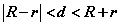 时,圆 时,圆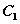 与圆 与圆 相交; 相交;
4° 当 时,圆 时,圆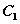 与圆 与圆 内切; 内切;
5° 当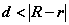 时,圆 时,圆 与圆 与圆 内含。 内含。
⑵代数方法:
由两圆的方程组成的方程组的实数解的个数判断。
1o 若方程组有两组不同的实数解,则两圆相交;
2o 若方程组有两组相同的实数解,则两圆相切;
3o 若无实数解,两圆相离。
⑶比较两种方法:
1o 几何方法直观,容易理解,但不能求出交点坐标。
2o 代数方法可以求出公共点,但不能准确地判断具体的位置关系,如有一个交点时不能判断内切还是外切,无交点时不能判断内含还是外离。
⑷判断方法的转化:
把两圆的位置关系判断转化为直线与圆的位置关系的判断,其步骤为:
1o 若将两个圆的方程相减,消去二次项,得到一个一元一次方程,即相交两圆的公共弦的直线方程。因为它过两圆的交点,过两圆的交点的直线是唯一的。
例如,相交两圆的方程为: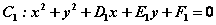 , , ,则其公共弦的直线方程为 ,则其公共弦的直线方程为 。 。
2o 两个圆的公共点的问题可以化归为这条公共弦的直线与两个圆中的一个圆的公共点的判定问题,于是可以由点到直线的距离公式与该圆的半径的大小做出判断。
|

