|
3.2.7 复合函数的单调性<-->3.2.9 函数奇偶性的判定方法
函数奇偶性定义
①严格定义:
对于函数$f(x)$的定义域内的任意一个$x$,都有$f(-x)=-f(x)$,那么函数$f(x)$就叫做奇函数。
对于函数$f(x)$的定义域内的任意一个$x$,都有$f(-x)=f(x)$,那么函数$f(x)$就叫做偶函数。
②定义内涵:
Ⅰ、在定义域内既存在$x$,又存在$-x$,所以其定义域必须关于原点对称。这构成了函数奇偶性的必要条件。
Ⅱ、奇函数:$f(-x)=-f(x) \Leftrightarrow f(-x)+f(x)=0$,或 $\dfrac{f(-x)}{f(x)}=-1$(若$f(x)≠0$)。
偶函数:$f(-x)=f(x) \Leftrightarrow f(-x)-f(x)=0$,或 $\dfrac{f(-x)}{f(x)}=1$(若$f(x)≠0$)。
Ⅲ、已知函数f(x)是奇函数,若f(0)有定义,则f(0)=0;偶函数则不一定,若f(x)是偶函数,则f(x)= f(-x)ó f(x)=f(|x|)。
③定义外延:
Ⅰ、奇偶性与单调性的关系:
奇函数在对称区间(-b,-a)与(a,b)上增减性相同;
偶函数在对称区间(-b,-a)与(a,b)上增减性相反。
Ⅱ、奇偶性与运算的关系:
设f(x),g(x)的定义域分别是D1 ,D2 ,那么在它们的公共定义域上奇偶性为:
奇+奇=奇,奇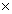 奇=偶,偶+偶=偶,偶 奇=偶,偶+偶=偶,偶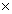 偶=偶,奇 偶=偶,奇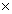 偶=奇。 偶=奇。
Ⅲ、奇偶性与复合函数的关系:
已知函数g(x),f(x),f[g(x)]的定义域都是关于原点对称的,
若u=g(x),y=f(u)都是奇函数时,则y=f[g(x)]是奇函数;
若u=g(x),y=f(u)都是偶函数,或者一奇一偶时,则y= f[g(x)]是偶函数。
函数奇偶性的几何特征
①定义域关于原点对称是函数奇偶性的必要条件。
②奇函数的图象关于原点成中心对称。

③偶函数的图象关于y轴对称。
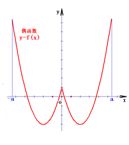
推广:如果对于函数f(x)的定义域内任意一个x,都有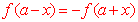 ,则f(x)的图象关于点 ,则f(x)的图象关于点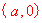 对称;如果对于函数f(x)的定义域内任意一个x,都有 对称;如果对于函数f(x)的定义域内任意一个x,都有 ,则f(x)的图象关于直线 ,则f(x)的图象关于直线 对称。 对称。
3.2.7 复合函数的单调性<-->3.2.9 函数奇偶性的判定方法
全网搜索"3.2.8 奇函数和偶函数"相关
|

