|
2023年高考数学乙卷-理4<-->2023年高考数学乙卷-理6
(5分)设$O$为平面坐标系的坐标原点,在区域$\{(x,y)\vert 1\leqslant x^{2}+y^{2}\leqslant 4\}$内随机取一点,记该点为$A$,则直线$OA$的倾斜角不大于$\dfrac{\pi }{4}$的概率为$($ $)$
A.$\dfrac{1}{8}$ B.$\dfrac{1}{6}$ C.$\dfrac{1}{4}$ D.$\dfrac{1}{2}$
答案:$C$
分析:作出图形,根据几何概型的概率公式,即可求解.
解:如图,$PQ$为第一象限与第三象限的角平分线,
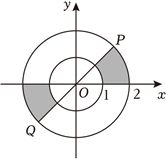
根据题意可得构成$A$的区域为圆环,
而直线$OA$的倾斜角不大于$\dfrac{\pi }{4}$的点$A$构成的区域为图中阴影部分,
$\therefore$所求概率为$\dfrac{2}{8}=\dfrac{1}{4}$.
故选:$C$.
点评:本题考查几何概型的概率的求解,属基础题.
2023年高考数学乙卷-理4<-->2023年高考数学乙卷-理6
全网搜索"2023年高考数学乙卷-理5"相关
|

