|
2023年高考数学甲卷-文22<-->返回列表
[选修4-5:不等式选讲]
23.设$a > 0$,函数$f(x)=2\vert x-a\vert -a$.
(1)求不等式$f(x) < x$的解集;
(2)若曲线$y=f(x)$与$x$轴所围成的图形的面积为2,求$a$.
答案:(1)$(\dfrac{a}{3}$,$3a)$.
(2)$a=2$.
分析:(1)根据绝对值的意义表示成分段函数,解不等式即可.
(2)作出$f(x)$的图象,求出交点坐标,利用三角形的面积公式进行求解即可.
解:(1)$\because a > 0$,$\therefore$当$x\geqslant a$时,$f(x)=2(x-a)-a=2x-3a$,
当$x < a$时,$f(x)=-2(x-a)-a=-2x+a$,
则当$x\geqslant a$时,由$f(x) < x$得$2x-3a < x$,$x < 3a$,此时$a\leqslant x < 3a$,
当$x < a$时,由$f(x) < x$得$-2x+a < x$,$x > \dfrac{\;a}{3}$,此时$\dfrac{a}{3} < x < a$,
综上$\dfrac{a}{3} < x < 3a$,即不等式的解集为$(\dfrac{a}{3}$,$3a)$.
(2)作出$f(x)$的图象如图:
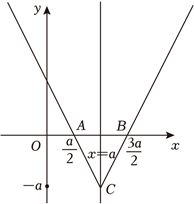
则$A(\dfrac{a}{2}$,$0)$,$B(\dfrac{3a}{2}$,$0)$,$C(a,-a)$,则$\vert AB\vert =\dfrac{3a}{2}-\dfrac{a}{2}=a$,
则$\Delta ABC$的高$h=a$,
则$S_{\Delta ABC}=\dfrac{1}{2}\cdot a\cdot a=2$,得$a^{2}=4$,即$a=2$.
点评:本题主要考查绝对值不等式的应用,将绝对值不等式表示为分段函数以及利用数形结合进行求解是解决本题的关键,是中档题.
2023年高考数学甲卷-文22<-->返回列表
全网搜索"2023年高考数学甲卷-文23"相关
|

