|
2022年高考数学上海春18<-->2022年高考数学上海春20
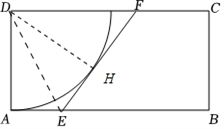
(14分)为有效塑造城市景观、提升城市环境品质,上海市正在努力推进新一轮架空线入地工程的建设.如图是一处要架空线入地的矩形地块$ABCD$,$AB=30m$,$AD=15m$.为保护$D$处的一棵古树,有关部门划定了以$D$为圆心、$DA$为半径的四分之一圆的地块为历史古迹封闭区.若空线入线口为$AB$边上的点$E$,出线口为$CD$边上的点$F$,施工要求$EF$与封闭区边界相切,$EF$右侧的四边形地块$BCFE$将作为绿地保护生态区.(计算长度精确到$0.1m$,计算面积精确到$0.01m^{2})$
(1)若$\angle ADE=20^\circ$,求$EF$的长;
(2)当入线口$E$在$AB$上的什么位置时,生态区的面积最大?最大面积是多少?

分析:(1)作$DH\bot EF$,然后结合锐角三角函数定义表示出$EF$,
(2)设$\angle ADE=\theta$,结合锐角三角函数定义可表示$AE$,$FH$,然后表示出面积,结合同角基本关系进行化简,再由基本不等式可求.
解:(1)作$DH\bot EF$,垂足为$H$,
则$EF=EH+HF=15\tan 20^\circ +15\tan 50^\circ \approx 23.3m$;
(2)设$\angle ADE=\theta$,则$AE=15\tan \theta$,$FH=15\tan (90^\circ -2\theta )$,
${{S}_{ADFE}}=2{{S}_{\Delta ADE}}+{{S}_{\Delta DFH}}=2\times \dfrac{1}{2}\times 15\times 15\tan\theta +\dfrac{1}{2}\times 15\times 15\tan\left( 90{}^\circ -2\theta \right)$,
$=\dfrac{15}{2}(30\tan \theta +15\cot 2\theta )=\dfrac{15}{2}(30\tan \theta +15\times \dfrac{1+\tan^{2}\theta }{2\tan \theta })=\dfrac{225}{4}(3\tan \theta +\dfrac{1}{\tan \theta })\geqslant \dfrac{225\sqrt{3}}{3}$,
当且仅当$3\tan \theta =\dfrac{1}{\tan \theta }$,即$\tan \theta =\dfrac{\sqrt{3}}{3}$时取等号,此时$AE=15\tan \theta =5\sqrt{3}$,最大面积为$450-\dfrac{225\sqrt{3}}{2}\approx 255.14m^{2}$.
点评:本题主要考查了利用基本不等式在求解最值中的应用,解题的关键是由实际问题抽象出数学问题,属于中档题.
2022年高考数学上海春18<-->2022年高考数学上海春20
全网搜索"2022年高考数学上海春19"相关
|

