|
2022年高考数学甲卷-文18<-->2022年高考数学甲卷-文20
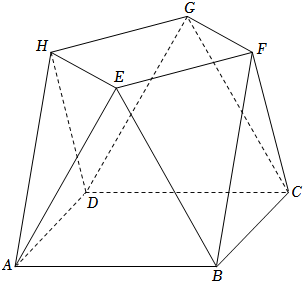
(12分)小明同学参加综合实践活动,设计了一个封闭的包装盒.包装盒如图所示:底面$ABCD$是边长为8(单位:$cm)$的正方形,$\Delta EAB$,$\Delta FBC$,$\Delta GCD$,$\Delta HDA$均为正三角形,且它们所在的平面都与平面$ABCD$垂直.
(1)证明:$EF//$平面$ABCD$;
(2)求该包装盒的容积(不计包装盒材料的厚度).
分析:(1)将几何体补形之后结合线面平行的判断定理即可证得题中的结论;
(2)首先确定几何体的空间特征,然后结合相关的棱长计算其体积即可.
(1)证明:如图所示,将几何体补形为长方体,

做$EE'\bot AB$于点$E'$,做$FF'\bot BC$于点$F'$,
由于底面为正方形,$\Delta ABE$,$\Delta BCF$均为等边三角形,
故等边三角形的高相等,即$EE'=FF'$,
由面面垂直的性质可知$EE'$,$FF'$均与底面垂直,
则$EE'//FF'$,四边形$EE'F'F$为平行四边形,则$EF//E'F'$,
由于$EF$不在平面$ABCD$内,$E'F'$在平面$ABCD$内,
由线面平行的判断定理可得$EF//$平面$ABCD$.
(2)解:易知包装盒的容积为长方体的体积减去四个三棱锥的体积,
其中长方体的高$AA_{1}=EE'=4\sqrt{3}$,
长方体的体积$V_{1}=8\times 8\times 4\sqrt{3}=256\sqrt{3}cm^{3}$,
一个三棱锥的体积$V_{2}=\dfrac{1}{3}\times (\dfrac{1}{2}\times 4\times 4)\times 4\sqrt{3}=\dfrac{32\sqrt{3}}{3}cm^{3}$,
则包装盒的容积为$V=V_{1}-4V_{2}=256\sqrt{3}-4\times \dfrac{32\sqrt{3}}{3}=\dfrac{640}{3}\sqrt{3}cm^{3}$.
点评:本题主要考查线面平行的判定,空间几何体体积的计算等知识,属于中等题.
2022年高考数学甲卷-文18<-->2022年高考数学甲卷-文20
全网搜索"2022年高考数学甲卷-文19"相关
|

