|
2021年高考数学天津19<-->返回列表
20.(16分)已知$a>0$,函数$f(x)=ax-xe^{x}$.
(1)求曲线$f(x)$在点$(0$,$f(0))$处的切线方程;
(2)证明函数$f(x)$存在唯一的极值点;
(3)若$\exists a$,使得$f(x)\leqslant a+b$对任意的$x\in R$恒成立,求实数$b$的取值范围.
分析:(1)先求导函数,然后根据导数的几何意义求出切线的斜率,最后利用点斜式表示出切线即可;
(2)令$f'(x)=0$,将$a$分离,然后利用导数研究另一侧函数的单调性,画出图象,可知当$a>0$时,$y=a$与$y=g(x)$仅有一个交点,然后判定在交点处左右导数符号,从而可得结论;
(3)由(2)知$f(x)_{max}=f(m)$,此时$a=(1+m)e^{m}$,$(m>-1)$,所以$\{f(x)-a\}_{max}=(m^{2}-m-1)e^{m}(m>-1)$,构造$h(x)=(x^{2}-x-1)e^{x}(x>-1)$,若存在$a$,使$f(x)\leqslant a+b$对任意的$x\in R$恒成立,则等价于存在$x\in (-1,+\infty )$,使得$h(x)\leqslant b$,即$b\geqslant h(x)_{min}$,最后利用导数研究其最值,即可求出所求.
(1)解:因为$f'(x)=a-(x+1)e^{x}$,所以$f'(0)=a-1$,而$f(0)=0$,
所以在$(0$,$f(0))$处的切线方程为$y=(a-1)x(a>0)$;
(2)证明:令$f'(x)=a-(x+1)e^{x}=0$,则$a=(x+1)e^{x}$,
令$g(x)=(x+1)e^{x}$,则$g'(x)=(x+2)e^{x}$,令$g'(x)=0$,解得$x=-2$,
当$x\in (-\infty ,-2)$时,$g'(x)<0$,$g(x)$单调递减,
当$x\in (-2,+\infty )$时,$g'(x)>0$,$g(x)$单调递增,
当$x\rightarrow -\infty$时,$g(x)<0$,当$x\rightarrow +\infty$时,$g(x)>0$,
作出图象
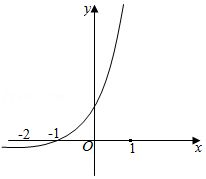
所以当$a>0$时,$y=a$与$y=g(x)$仅有一个交点,令$g(m)=a$,
则$m>-1$,且$f(m)=a-g(m)=0$,
当$x\in (-\infty ,m)$时,$a>g(m)$,$f'(x)>0$,$f(x)$为增函数;
当$x\in (m,+\infty )$时,$a<g(m)$,$f'(x)<0$,$f(x)$为减函数;
所以$x=m$时$f(x)$的极大值点,故$f(x)$仅有一个极值点;
(3)解:由(2)知$f(x)_{max}=f(m)$,
此时$a=(1+m)e^{m}$,$(m>-1)$,
所以$\{f(x)-a\}_{max}=f(m)-a=(1+m)e^{m}-m-me^{m}-(1+m)e^{m}=(m^{2}-m-1)e^{m}(m>-1)$,
令$h(x)=(x^{2}-x-1)e^{x}(x>-1)$,
若存在$a$,使$f(x)\leqslant a+b$对任意的$x\in R$恒成立,
则等价于存在$x\in (-1,+\infty )$,使得$h(x)\leqslant b$,即$b\geqslant h(x)_{min}$,
而$h'(x)=(x^{2}+x-2)e^{x}=(x-1)(x+2)e^{x}$,$(x>-1)$,
当$x\in (-1,1)$时,$h'(x)<0$,$h(x)$为单调减函数,
当$x\in (1,+\infty )$时,$h'(x)>0$,$h(x)$为单调增函数,
所以$h(x)_{min}=h$(1)$=-e$,故$b\geqslant -e$,
所以实数$b$的取值范围$[-e$,$+\infty )$.
点评:本题主要考查了利用导数研究函数在某点处的切线,以及利用导数研究极值与最值,同时考查了转化能力和运算求解的能力,属于中档题.
2021年高考数学天津19<-->返回列表
全网搜索"2021年高考数学天津20"相关
|

