|
2021年高考数学甲卷-理18<-->2021年高考数学甲卷-理20
19.(12分)已知直三棱柱$ABC-A_{1}B_{1}C_{1}$中,侧面$AA_{1}B_{1}B$为正方形,$AB=BC=2$,$E$,$F$分别为$AC$和$CC_{1}$的中点,$D$为棱$A_{1}B_{1}$上的点,$BF\bot A_{1}B_{1}$.
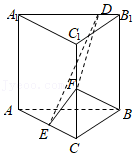
(1)证明:$BF\bot DE$;
(2)当$B_{1}D$为何值时,面$BB_{1}C_{1}C$与面$DFE$所成的二面角的正弦值最小?
分析:(1)连接$AF$,易知$CF=1$,$BF=\sqrt{5}$,由$BF\bot A_{1}B_{1}$,$BF\bot AB$,再利用勾股定理求得$AF$和$AC$的长,从而证明$BA\bot BC$,然后以$B$为原点建立空间直角坐标系,证得$\overrightarrow{BF}\cdot \overrightarrow{DE}=0$,即可;
(2)易知平面$BB_{1}C_{1}C$的一个法向量为$\overrightarrow{p}=(1$,0,$0)$,求得平面$DEF$的法向量$\overrightarrow{n}$,再由空间向量的数量积可得$\cos <\overrightarrow{p}$,$\overrightarrow{n}>=\dfrac{3}{\sqrt{2(m-\dfrac{1}{2})^{2}+\dfrac{27}{2}}}$,从而知当$m=\dfrac{1}{2}$时,得解.
(1)证明:连接$AF$,
$\because E$,$F$分别为直三棱柱$ABC-A_{1}B_{1}C_{1}$的棱$AC$和$CC_{1}$的中点,且$AB=BC=2$,
$\therefore CF=1$,$BF=\sqrt{5}$,
$\because BF\bot A_{1}B_{1}$,$AB//A_{1}B_{1}$,
$\therefore BF\bot AB$
$\therefore AF=\sqrt{A{B}^{2}+B{F}^{2}}=\sqrt{{2}^{2}+(\sqrt{5})^{2}}=3$,$AC=\sqrt{A{F}^{2}-C{F}^{2}}=\sqrt{{3}^{2}-{1}^{2}}=2\sqrt{2}$,
$\therefore AC^{2}=AB^{2}+BC^{2}$,即$BA\bot BC$,
故以$B$为原点,$BA$,$BC$,$BB_{1}$所在直线分别为$x$,$y$,$z$轴建立如图所示的空间直角坐标系,
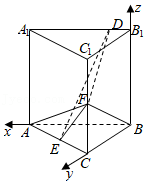
则$A(2$,0,$0)$,$B(0$,0,$0)$,$C(0$,2,$0)$,$E(1$,1,$0)$,$F(0$,2,$1)$,
设$B_{1}D=m$,则$D(m$,0,$2)$,
$\therefore$$\overrightarrow{BF}=(0$,2,$1)$,$\overrightarrow{DE}=(1-m$,1,$-2)$,
$\therefore$$\overrightarrow{BF}\cdot \overrightarrow{DE}=0$,即$BF\bot DE$.
(2)解:$\because AB\bot$平面$BB_{1}C_{1}C$,$\therefore$平面$BB_{1}C_{1}C$的一个法向量为$\overrightarrow{p}=(1$,0,$0)$,
由(1)知,$\overrightarrow{DE}=(1-m$,1,$-2)$,$\overrightarrow{EF}=(-1$,1,$1)$,
设平面$DEF$的法向量为$\overrightarrow{n}=(x$,$y$,$z)$,则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{DE}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{EF}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{(1-m)x+y-2z=0}\\ {-x+y+z=0}\end{array}\right.$,
令$x=3$,则$y=m+1$,$z=2-m$,$\therefore$$\overrightarrow{n}=(3$,$m+1$,$2-m)$,
$\therefore \cos <\overrightarrow{p}$,$\overrightarrow{n}>=\dfrac{\overrightarrow{p}\cdot \overrightarrow{n}}{\vert \overrightarrow{p}\vert \cdot \vert \overrightarrow{n}\vert }=\dfrac{3}{1\times \sqrt{9+(m+1)^{2}+(2-m)^{2}}}=\dfrac{3}{\sqrt{2{m}^{2}-2m+14}}=\dfrac{3}{\sqrt{2(m-\dfrac{1}{2})^{2}+\dfrac{27}{2}}}$,
$\therefore$当$m=\dfrac{1}{2}$时,面$BB_{1}C_{1}C$与面$DFE$所成的二面角的余弦值最大,此时正弦值最小,
故当$B_{1}D=\dfrac{1}{2}$时,面$BB_{1}C_{1}C$与面$DFE$所成的二面角的正弦值最小.
点评:本题考查空间中线与线的垂直关系,二面角的求法,熟练掌握利用空间向量证明线线垂直和求二面角的方法是解题的关键,考查空间立体感、推理论证能力和运算能力,属于中档题.
2021年高考数学甲卷-理18<-->2021年高考数学甲卷-理20
全网搜索"2021年高考数学甲卷-理19"相关
|

