|
2021年高考数学甲卷-理15<-->2021年高考数学甲卷-理17
16.(5分)已知函数$f(x)=2\cos (\omega x+\varphi )$的部分图像如图所示,则满足条件$(f(x)-f(-\dfrac{7\pi }{4}))(f(x)-f(\dfrac{4\pi }{3}))>0$的最小正整数$x$为______.
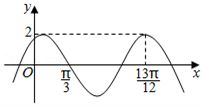
分析:观察图像,$\dfrac{3}{4}T=\dfrac{13\pi }{12}-\dfrac{\pi }{3}$,即周期为$\pi$,将需要求解的式子进行周期变换,变换到$\dfrac{\pi }{3}$附近,观察图像可知$x>\dfrac{\pi }{3}$,即最小正整数为2.
解:由图像可得$\dfrac{3}{4}T=\dfrac{13}{12}\pi -\dfrac{\pi }{3}$,即周期为$\pi$,
$\because$$(f(x)-f(-\dfrac{7\pi }{4}))((f(x)-f(\dfrac{4\pi }{3}))>0$,$T=\pi$,
$\therefore$$(f(x)-f(\dfrac{\pi }{4}))(f(x)-f(\dfrac{\pi }{3}))>0$,
观察图像可知当$x>\dfrac{\pi }{3}$,
$f(x)<f(\dfrac{\pi }{4})$,$f(x)<f(\dfrac{\pi }{3})$,
$\because 2\in (\dfrac{\pi }{3},\dfrac{5\pi }{6})$,且$f(\dfrac{5\pi }{6})=0$,
$\therefore x=2$时最小,且满足题意,
故答案为:2.
点评:该题考查了三角函数的周期性,以及如何通过图像判断函数值的大小,题型灵活,属于中等题.
2021年高考数学甲卷-理15<-->2021年高考数学甲卷-理17
全网搜索"2021年高考数学甲卷-理16"相关
|

