本题主要考查函数与方程。
由题意,$g(x)=\begin{cases} e^x+x+a,x \leqslant 0\\ \text{ln}x+x+a,x>0 \end{cases}$,
$g(x)$存在$2$个零点即$g(x)=0$存在两个解;
当$x \leqslant 0$时,$g(x)=e^x+x+a=0$的解等价于$h(x)=e^x+x$与$y=-a$的交点个数($x \leqslant 0$),
因为$h'(x)=e^x+1>0$,所以$h(x)$在$(-\infty ,0]$上单调递增,
所以$h(x)_{max}=h(0)=1$,
当$x \to -\infty$时,$h(x) \to -\infty$;
当$x>0$时,$g(x)=\text{ln}x+x+a=0$的解等价于$\varphi(x)=\text{ln}x+x$与$y=-a$的交点个数($x>0$),
因为$x>0$时,$\varphi'(x)=\dfrac{1}{x}+1>0$,所以$\varphi(x)$在$(0,+\infty)$上单调递增,
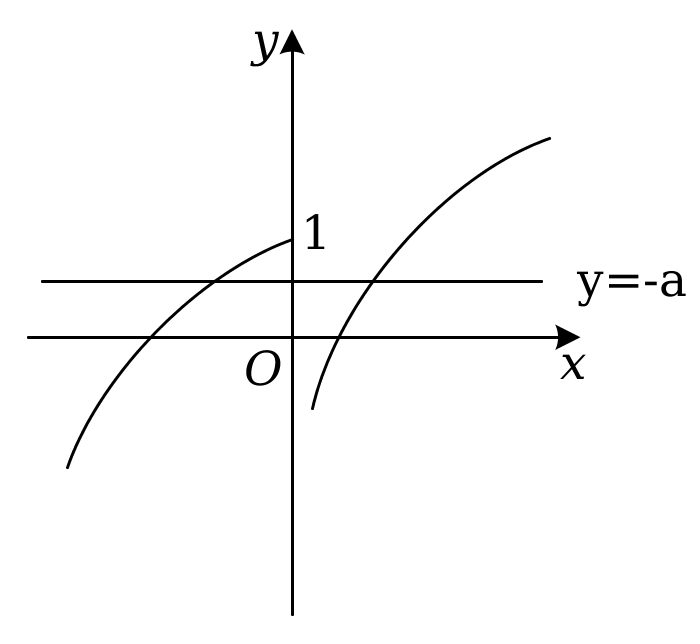
画出函数$F(x)=\begin{cases} h(x),x \leqslant 0\\ \varphi(x),x>0 \end{cases}$的图象如图所示,
要使$g(x)$存在$2$个零点,则$-a \leqslant 1$,即$a\geqslant -1$。
故本题正确答案为C。

