(2017天津卷计算题)(本小题满分13分)
电视台播放甲、乙两套连续剧,每次播放连续剧时,需要播放广告。已知每次播放甲、乙两套连续剧时,连续剧播放时长、广告播放时长、收视人次如表所示:

已知电视台每周安排的甲、乙连续剧的总播放时间不多于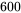 分钟,广告的总播放时间不少于
分钟,广告的总播放时间不少于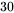 分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的
分钟,且甲连续剧播放的次数不多于乙连续剧播放次数的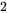 倍。分别用
倍。分别用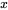 ,
,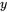 表示每周计划播出的甲、乙两套连续剧的次数。
表示每周计划播出的甲、乙两套连续剧的次数。
(Ⅰ)用,、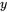 列出满足题目条件的数学关系式,并画出相应的平面区域;
列出满足题目条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问电视台每周播出甲、乙两套连续剧各多少次,才能使总收视人次最多?
【出处】
