|
1.1.3数集<-->1.1.5相反数
(1)数轴的定义:
在数学中人们用画图的方式把数“直观化”通常用一条直线上的点表示数,这条直线叫做数轴,它满足以下要求:
①在直线上任取一个点表示数0,这个点叫做原点;
②通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
③选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似的方法依次表示-1,-2,-3,…(如图 )
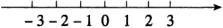
数轴有三要素——原点、正方向和单位长度,数轴三要素缺一不可,只具备其中两个要素或一个要素的直线不是数轴.
注意:
a.原点的位置、单位长度的大小可根据实际情况适当选取,但同一数轴的单位长度要一致.
b.确定单位长度时,根据实际情况,有时也可以每隔两个(或更多的)单位长度取一点,如从原点向右,依次表示为2,4.6,…;从原点向左,依次表示为 -2,-4,-6,(如图 ).

(2)数轴上的点与有理数的关系:
数轴是数形结合的基础,能把数与直线上的点生动形象地联系起来,有了数轴,任何一个有理数都可以用数轴上的一个确定的点来表示.正有理数可以用原点右边的点表示,负有理数可以用原点左边的点表示,零用原点表示.
注意:
有理数都可以用数轴上的点来表示,但数轴上的点表示的不都是有理数.
1.1.3数集<-->1.1.5相反数
全网搜索"1.1.4数轴"相关
|

