| 2023年高考数学上海20 |
|
2023-07-08 14:29:52 |
|
|
(18分)已知抛物线$\Gamma :y^{2}=4x$,在$\Gamma$上有一点$A$位于第一象限,设$A$的纵坐标为$a(a > 0)$.
(1)若$A$到抛物线$\Gamma$准线的距离为3,求$a$的值;
(2)当$a=4$时,若$x$轴上存在一点$B$,使$AB$的中点在抛物线$\Gamma$上,求$O$到直线$AB$的距离;
(3)直线$l:x=-3$,抛物线上有一异于点$A$的动点$P$,$P$在直线$l$上的投影为点$H$,直线$AP$与直线$l$的交点为$Q$.若在$P$的位置变化过程中,$\vert HQ\vert > 4$恒成立,求$a$的取值范围.
答案:(1)$a=2\sqrt{2}$;(2)$\dfrac{4\sqrt{13}}{13}$;(3)$(0$,$2]$.
分析:(1)根据题意可得点$A$的横坐标为2,将其代入抛物线的方程,即可求得$a$的值;
(2)易知$A(4,4)$,设$B(b,0)$,由$AB$的中点在抛物线上,可得$b$的值,进而得到直线$AB$的方程,再由点到直线的距离公式得解;
(3)设$P(\dfrac{{t}^{2}}{4},t),A(\dfrac{{a}^{2}}{4},a),H(-3,t)(t\ne a)$,表示出直线$AP$的方程,进一步表示出点$Q$的坐标,再根据$\vert HQ\vert > 4$恒成立,结合基本不等式即可得到$a$的范围.
解:(1)抛物线$\Gamma :y^{2}=4x$的准线为$x=-1$,
由于$A$到抛物线$\Gamma$准线的距离为3,
则点$A$的横坐标为2,则$a^{2}=4\times 2=8(a > 0)$,
解得$a=2\sqrt{2}$;
(2)当$a=4$时,点$A$的横坐标为$\dfrac{{4}^{2}}{4}=4$,则$A(4,4)$,
设$B(b,0)$,则$AB$的中点为$(\dfrac{b+4}{2},2)$,
由题意可得${2}^{2}=4\times \dfrac{b+4}{2}$,解得$b=-2$,
所以$B(-2,0)$,
则${k}_{AB}=\dfrac{4-0}{4+2}=\dfrac{2}{3}$,
由点斜式可得,直线$AB$的方程为$y=\dfrac{2}{3}(x+2)$,即$2x-3y+4=0$,
所以原点$O$到直线$AB$的距离为$\dfrac{4}{\sqrt{{2}^{2}+{3}^{2}}}=\dfrac{4\sqrt{13}}{13}$;
(3)如图,
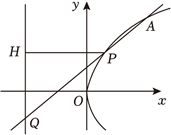
设$P(\dfrac{{t}^{2}}{4},t),A(\dfrac{{a}^{2}}{4},a),H(-3,t)(t\ne a > 0)$,则${k}_{AP}=\dfrac{t-a}{\dfrac{{t}^{2}}{4}-\dfrac{{a}^{2}}{4}}=\dfrac{4}{t+a}$,
故直线$AP$的方程为$y-a=\dfrac{4}{t+a}(x-\dfrac{{a}^{2}}{4})$,
令$x=-3$,可得$y=a-(\dfrac{{a}^{2}}{4}+3)\cdot \dfrac{4}{t+a}$,即$Q(-3,a-(\dfrac{{a}^{2}}{4}+3)\cdot \dfrac{4}{t+a})$,
则$\vert HQ\vert =\vert t-a+(\dfrac{{a}^{2}}{4}+3)\cdot \dfrac{4}{t+a}\vert$,
依题意,$\vert t-a+(\dfrac{{a}^{2}}{4}+3)\cdot \dfrac{4}{t+a}\vert > 4$恒成立,
又$t+a+(\dfrac{{a}^{2}}{4}+3)\cdot \dfrac{4}{t+a}-2a\geqslant 4\sqrt{\dfrac{{a}^{2}}{4}+3}-2a > 0$,
则最小值为$4\sqrt{\dfrac{{a}^{2}}{4}+3}-2a > 4$,即$2\sqrt{\dfrac{{a}^{2}}{4}+3} > 2+a$,即$\sqrt{{a}^{2}+12} > 2+a$,
则$a^{2}+12 > a^{2}+4a+4$,解得$0 < a < 2$,
又当$a=2$时,$t+2+\dfrac{16}{t+2}-4\geqslant 2\sqrt{(t+2)\cdot \dfrac{16}{t+2}}-4=4$,当且仅当$t=2$时等号成立,
而$a\ne t$,即当$a=2$时,也符合题意.
故实数$a$的取值范围为$(0$,$2]$.
点评:本题考查抛物线的定义及其性质,考查直线与抛物线的综合运用,考查运算求解能力,属于中档题.
|
|
http://x.91apu.com//shuxue/gkt/2023/2023sh/2023-07-08/33815.html |

