（14分）已知直四棱柱$ABCD-A_{1}B_{1}C_{1}D_{1}$，$AB\bot AD$，$AB//CD$，$AB=2$，$AD=3$，$CD=4$．
（1）证明：直线$A_{1}B//$平面$DCC_{1}D_{1}$；
（2）若该四棱柱的体积为36，求二面角$A_{1}-BD-A$的大小．

答案：（1）证明见解答；（2）$\arctan \dfrac{2\sqrt{13}}{3}$．
分析：（1）先证明平面$A_{1}ABB_{1}//$平面$DCC_{1}D_{1}$，再根据面面平行的性质，即可证明；
（2）先根据体积建立方程求出$A_{1}A=4$，再利用三垂线定理作出所求二面角的平面角，最后再解三角形，即可求解．
解：（1）证明：根据题意可知$AB//DC$，$AA_{1}//DD_{1}$，且$AB\bigcap AA_{1}=A$，
$\therefore$可得平面$A_{1}ABB_{1}//$平面$DCC_{1}D_{1}$，又直线$A_{1}B\subset$平面$A_{1}ABB_{1}$，
$\therefore$直线$A_{1}B//$平面$DCC_{1}D_{1}$；
（2）设$AA_{1}=h$，则根据题意可得该四棱柱的体积为$\dfrac{1}{2}\times (2+4)\times 3\times h=36$，
$\therefore h=4$，$\because A_{1}A\bot$底面$ABCD$，在底面$ABCD$内过$A$作$AE\bot BD$，垂足点为$E$，

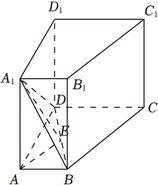
则$A_{1}E$在底面$ABCD$内的射影为$AE$，
$\therefore$根据三垂线定理可得$BD\bot A_{1}E$，
故$\angle A_{1}EA$即为所求，
在$\rm{Rt}\Delta ABD$中，$AB=2$，$AD=3$，$\therefore BD=\sqrt{4+9}=\sqrt{13}$，
$\therefore AE=\dfrac{AB\times AD}{BD}=\dfrac{2\times 3}{\sqrt{13}}=\dfrac{6}{\sqrt{13}}$，又$A_{1}A=h=4$，
$\therefore \tan \angle A_{1}EA=\dfrac{{A}_{1}A}{AE}=\dfrac{4}{\dfrac{6}{\sqrt{13}}}=\dfrac{2\sqrt{13}}{3}$，
$\therefore$二面角$A_{1}-BD-A$的大小为$\arctan \dfrac{2\sqrt{13}}{3}$．

点评：本题考查线面平行的证明，面面平行的判定定理与性质，二面角的求解，三垂线定理作二面角，化归转化思想，属中档题．