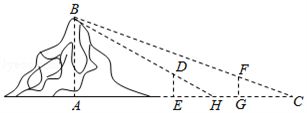
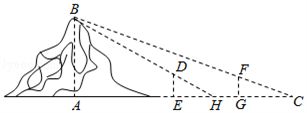
9．（5分）魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作，其中第一题是测量海岛的高．如图，点$E$，$H$，$G$在水平线$AC$上，$DE$和$FG$是两个垂直于水平面且等高的测量标杆的高度，称为“表高”， $EG$称为“表距”， $GC$和$EH$都称为“表目距”， $GC$与$EH$的差称为“表目距的差”，则海岛的高$AB=$(　　)

A．$\dfrac{\text{表高}\times \text{表距}}{\text{表目距的差}}+$表高              B．$\dfrac{\text{表高}\times \text{表距}}{\text{表目距的差}}-$表高              
C．$\dfrac{\text{表高}\times \text{表距}}{\text{表目距的差}}+$表距              D．$\dfrac{\text{表高}\times \text{表距}}{\text{表目距的差}}-$表距
分析：根据相似三角形的性质、比例的性质、直角三角形的边角关系即可得出．
解：$\dfrac{DE}{AB}=\dfrac{EH}{AH}$，$\dfrac{FG}{BA}=\dfrac{CG}{CA}$，故$\dfrac{EH}{AH}=\dfrac{CG}{CA}$，即$\dfrac{EH}{AE+EH}=\dfrac{CG}{AE+EG+GC}$，
解得$AE=\dfrac{EH\cdot EG}{CG-EH}$，$AH=AE+EH$，
故$AB=\dfrac{DE\cdot AH}{EH}=\dfrac{DE\left( AE+EH \right)}{EH}=\dfrac{\;DE\cdot AE}{EH}+\dfrac{DE\cdot EH}{EH}=\dfrac{DE\cdot EG}{CG-EH}+DE=\dfrac{\text{表高}\times \text{表距}}{\text{表目距的差}}+$表高．
故选：$A$．

点评：本题考查了相似三角形的性质、比例的性质、直角三角形的边角关系，考查了推理能力与计算能力，属于中档题．