|
变换的复合与矩阵的乘法
1.复合变换
定义:一般地,设A、B是平面上的两个变换,将平面上每个点P先用变换A变到 ,再用变换B将 ,再用变换B将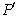 变成 变成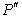 ,则从P到 ,则从P到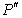 也是平面上的一个变换,称为A,B的复合变换,也称为B与A的乘积,记作BA. 也是平面上的一个变换,称为A,B的复合变换,也称为B与A的乘积,记作BA.
注意:这里先施行变换A,后施行变换B,但它们的复合变换要记作BA而不记作AB.
变换的乘法不满足交换律。即 . .
2.矩阵的乘法:设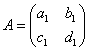 , ,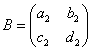 ,则 ,则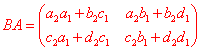 . .
规则:将行向量的两个数与列向量的两个数分别对应相乘,再将所得的乘积相加,这个规则其实就是求两个向量的数量积的规则。
将矩阵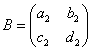 的第i行( 的第i行(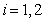 )与矩阵 )与矩阵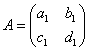 的第j( 的第j(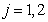 )列相乘得到一个数,得到的就是矩阵BA的第i行、第j列的数。 )列相乘得到一个数,得到的就是矩阵BA的第i行、第j列的数。
如:B的第一行乘以A的第一列得到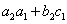 ; ;
B的第一行乘以A的第二列得到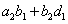 ; ;
B的第二行乘以A的第一列得到 ; ;
B的第二行乘以A的第二列得到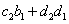 . .
矩阵的乘法同样不满足交换律。即 ,此式子不一定成立。 ,此式子不一定成立。
|

