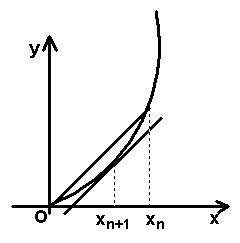|
一、复习目标 了解导数概念的某些实际背景(瞬时速度,加速度,光滑曲线切线的斜率等),掌握函数在一点处的导数的定义和导数的几何意义,理解导函数的概念,熟记基本的导数公式`(c,x^m(m为有理数),sinx,cosx,e^x,lnx,log_a x`的导数),并能熟练应用它们求有关导数. 二、重点难点 (这里输入) 三、特别提示 |
| 知识梳理
1、导数的概念 |
|
应用举例 一、 应用特点 1、函数在某一点处导数的定义及几何意义的应用 2、用函数的求导法则和基本求导公式解题 3、灵活应用求导法解题
二、案例示范
1、 已知曲线`y=x+1/x`上一点`A(2,5/2)`,用导数的定义求:
2、求下列各函数的导数,(1)`y=(1+2x^8)^8`;(2)`y=ln sqrt((x-1)/(x+1))(x>1);(3)`y=e^(sinx·lnx)`.
3、已知`f(1/x)=x/(1+x)`,求`f'(x)`
|
| 实践体验 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高.) 1、已知曲线`C:y=x^3-3x^2+2x`,直线`l:y=kx`,且直线l与曲线C相切于点`(x_0,y_0)(x_0!=0)`,求直线l的方程及切点坐标.
2、设`f(x)`是定义在`RR`上的函数,且对任何`x_1、x_2 in RR`都有`f(x_1+x_2)=f(x_1)?f(x_2)`,若`f(0)!=0, f'(0)=1` (1)求`f(0)`的值; (2)证明对任何`x in RR`,都有`f(x)=f'(x)`.
|
| 拓展探究 1、求下列复合函数的导数. (1)`y=((sin2x)/cosx^2)^3`; (2)`y=root(3)((x-2)/(2x+1))`; (3)`y=sqrt(1+cos^2(x^2))`;
|
|
|
|
|
学习感悟 |