|
一、复习目标 了解球的概念,掌握球的性质,掌握球的表面积和体积公式. 了解经度、纬度和球面距离的概念.
二、重点难点 三、特别提示
(2)球的大圆含有球的全部计算元素,故有关球的计算问题,通常先作出球的大圆,然后利用平面几何知识求解.
(3)计算或证明中要注意联系球的半径、截面圆的半径及球心到截面的距离三者的关系,重视球的截面(含球的切面)的性质.
(4)注意球面上两点的直线距离、球面距离以及在相应的小圆上的弧长三者之间的区别与联系.特别注意球面距离,其关键是求出球面上两点与球心的张角(用弧度制表示),常常是结合直观图综合运用三角知识求解. (5)对于与球有关的组合体,应根据题意选择最佳角度作出轴截面图形,把复杂的图形分解为简单的图形,把中间图形问题转化为平面图形问题,实现这一转化要有丰富的空间想象力. |
|
知识梳理
1、多面体与正多面体 (2)凸多面休:把一个多面体的任一个面伸展成平面,如果其余的面都位于这个平面的同一侧,这样的多面体叫做凸多面体. (3)正多面体:每个面都是有相同边数的正多边形,每个顶点为端点都有相同棱数的凸多面体,叫做正多面体.
2、球
(2)球的截面的性质 ②球心到截面圆心的连线叫圆心距; ③球心到截面的距离`d`与球的半径`R`及截面的半径`r`,有下面的关系:`r=sqrt(R^2-d^2)`
(3)球面距离:球面上两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,这个弧长叫做两点的球面距离. (4)球面面积`S_(球面)=4piR^2`;球体积`V_(球)=4/3piR^3`. |
|
应用举例
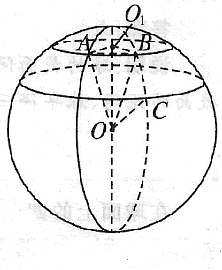
二、案例示范 1、如图,地球半径为`R`,地面上三点`A、B、C`的经纬度分别是:`A`点是东经`20°`,北纬`60°`;`B`点是东经`140°`,北纬`60°`;`C`点是东经`140°`,北纬`30°`,试求`A、B`与`B、C`两点的球面距离.
2、已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( ) A.`16pi` B.`20pi` C.`24pi` D.`32pi`
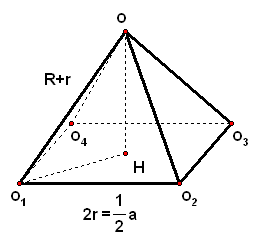
3、在棱长为`a`的正方体盒内装有五个球,其中四个是半径为`r`的等球,放在盒底四角,另一个大球半径为`R`,放在四个等球的上面.若四个等球相邻两个外切,且还与正方体的侧面及下底面相切,而这个大球分别与这四个等球相切,且与上底面相切,试用`a`表示`R、r`
|
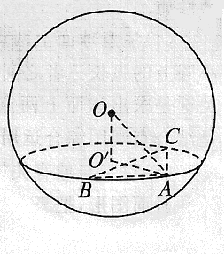
| 实践体验 在实践中提高能力,在体验中反思感悟,力求独立,力求提高 1、已知球的表面积为`20pi`,球面上有`A、B、C`三点,如果`AB=AC=2,BC=2sqrt3`,则球心到平面`ABC`的距离为( ) A.1 B.`sqrt2` C.`sqrt3` D.2
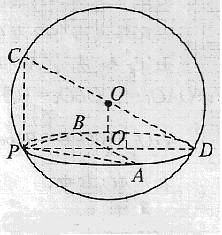
2、在球面上的四个点`P、A、B、C`,如果`PA、PB、PC`两两互相垂直,且`PA=PB=PC=a`,求这个球的表面积与体积.
|
|
拓展探究
|
|
|
|
|
学习感悟 |