|
一、复习目标
二、重点难点 三、特别提示 |
|
知识梳理
一、棱柱的概念及相关问题 但是,要注意“有两个面互相平行,其余各面都是平行四边形的几何体”不一定是棱柱.如图的几何体有两个面平行,其余各面都是平行四边形,但它不满足“每相邻两个侧面的公共边互相平行”.所以,它不是棱柱.
4、特殊的四棱柱 四棱柱`stackrel"底面为平行四边形"->`平行六面体`stackrel"侧棱垂直于底面"->`直棱柱
二、棱锥的概念及相关问题 1、棱锥的概念 有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥. 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥.
2、棱锥的性质 (1)正棱锥的性质 ①各侧棱相等,各侧面都是全等的等腰三角形. ②正棱锥的高、斜高、和斜高在底面内的射影组成一个直角三角形;正棱锥的高、侧棱、和侧棱在底面内的射影也组成一个直角三角形.
(2)一般棱锥的性质 定理:如果棱锥被平行于棱锥底面的平面所截,那么截面和底面相似,并且它们面积的比等于顶点到截面距离与棱锥高的平方比.
3、棱锥的体积 `V=1/3Sh`,其中`S`是棱锥的底面积,`h`是高. |
|
应用举例
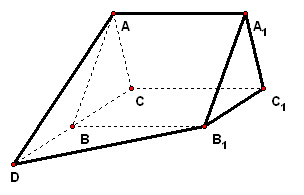
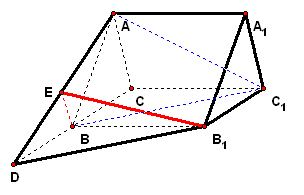
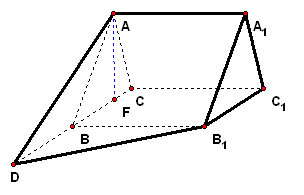
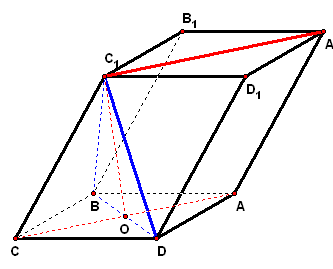
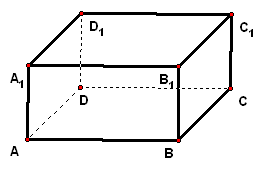
二、案例示范 1、如图,正三棱柱`ABC-A_1B_1C_1`的底面边为3,侧棱`A A_1=(3sqrt3)/2`,`D`是`CB`延长线上的一点,且`BD=BC`
2、在四棱锥`P-ABCD`中,底面是边长为2的菱形,`/_DAB=60°`,对角线`AC`与`BD`相交于点`O`,`PO_|_`平面`ABCD`,`PB`与平面`ABCD`所成的角为`60°` (1)求四棱锥`P-ABCD`的体积
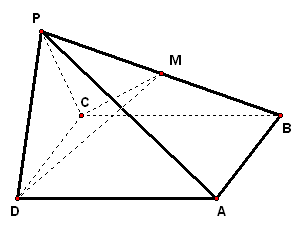
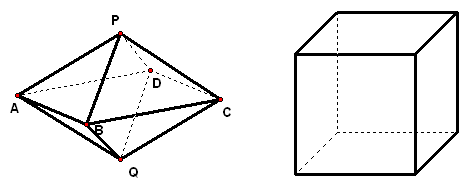
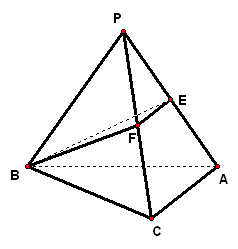
3、如图,`M`为正三棱锥`P-ABC`侧棱`PA`上任一点,若底面边长为12,`P`到底面的距离8,求截面`MBC`面积的最小值
|
| 实践体验 在实践中提高能力,在体验中反思感悟,力求独立,力求提高 1、设棱台上、下底面积分别为`S_1、S_2`,一个平行于底面的截面将棱台的高分为两部分,这上、下两部分的长之比为`lambda`,则截面面积为( ) A.`(S_1+lambdaS_2)/(1+lambda)` B.`(S_2+lambdaS_1)/(1+lambda)` C.`(sqrt(S_1)+lambdasqrt(S_2))/(1+lambda)` D.`(sqrt(S_2)+lambdasqrt(S_1))/(1+lambda)`
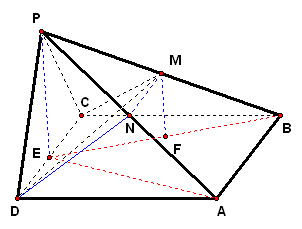
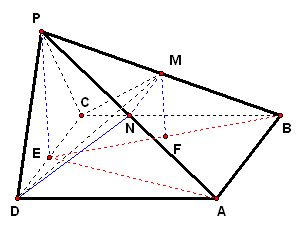
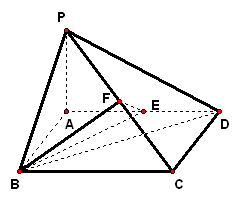
2、如图,在四棱锥`P-ABCD`中,侧面`PCD`是正三角形,且与底面`ABCD`垂直 .已知底面`ABCD`是面积为`2sqrt3`的菱形,`/_ADC=60°`,`M`是`PB`的中点.
|
|
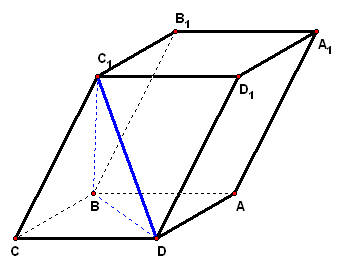
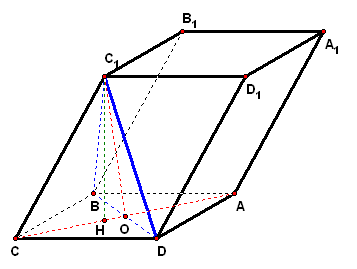
拓展探究 (1)证明:`C C_1_|_BD`
|
|
|
|
|
学习感悟 2、在涉及棱柱有关计算中,常会出现—些未知的几何量,此时应注意方程思想的应用,即适当地选取未知数,找出等量关系,转化为代数方程求解;对于非特殊图形的侧面积,往往采用“分解”的思路,分别求出各个侧面的面积. 3、在熟练掌握棱锥的定义、性质以及侧面和体积公式的同时,一定要注意综合运用知识.立体几何学科特点决定立体几何问题解答模式为推理论证和计算求解相结合,一般按照“作(作图)、证(证明)、述(必要的文字叙述)、算(计算求解)程序进行. 4、要学会识图、理解图、利用图,要善于从图形中发现需要的东西. 5、注意转化思想的运用,比如用等积法(面积、体积)割补法变换求解体积或距离问题. |