|
一、复习目标 二、重点难点 三、特别提示
|
|
知识梳理 两个平面垂直 1、定义:两个平面相交,如果它们的二面角是直二面角,就说这两个平面互相垂直. 2、判定定理:`{:(lsubalpha),(l_|_beta):}}rArralpha_|_beta` 3、性质定理:`{:(alpha_|_beta),(alphannbeta=m),(lsubalpha),(l_|_m):}}rArrl_|_beta` |
|
应用举例
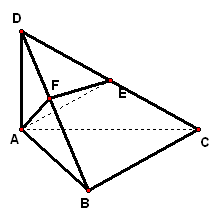
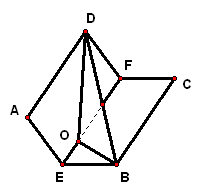
二、案例示范 1、在四面体`ABCD`中,`DA_|_平面ABC,/_ABC=90°,AE_|_CD,AF_|_DB` 求证:(1)`EF_|_DC`;(2)`平面DBC_|_平面AEF`
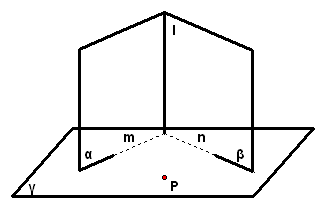
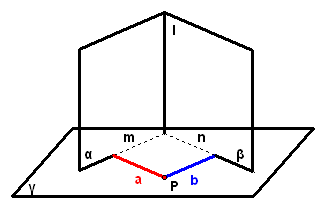
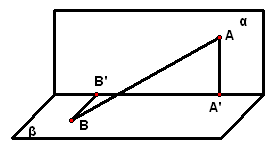
2、如图,已知`alphannbeta=l,alpha_|_gamma,beta_|_gamma,求证:l_|_gamma`
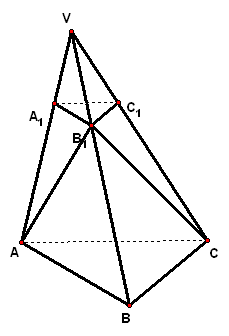
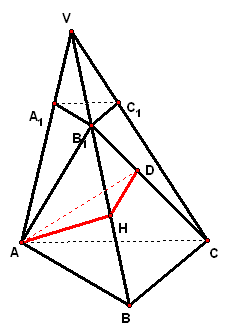
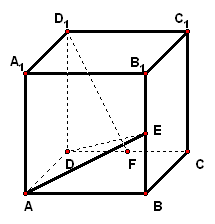
3、(2006·山东理)已知平面`A_1B_1C_1`平行于三棱锥`V-ABC`的 底面`ABC`,等边`△AB_1C`所在的平面与底面`ABC`垂直,且`/_ACB=90°`设`AC=2a,BC=a`
|
|
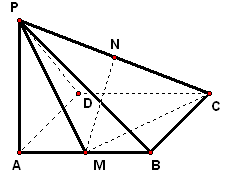
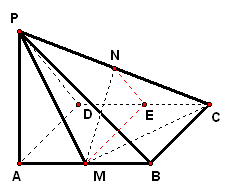
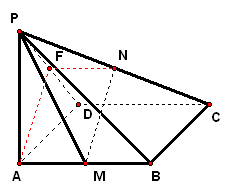
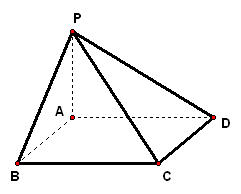
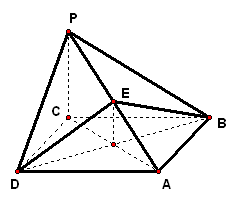
实践体验 1、已知`PA`垂直于矩形`ABCD`所在平面,`M`、`N`分别是`AB`、`PC`的中点,若`/_PDA=45°` 求证:`MN_|_平面PCD`
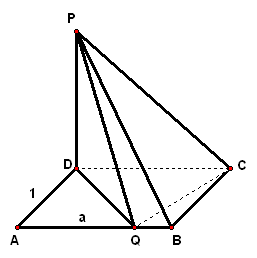
2、在矩形`ABCD`中,`AB=1`,`BC=a`,`PA_|_`平面`ABCD`,且`PA=1`,问`BC`边上是否一定存在点`Q`,使得`PQ_|_QD`?为什么?
|
|
拓展探究
|
|
|
|
|
学习感悟 |