|
一、复习目标 二、重点难点 三、特别提示
(5)注意掌握好以下几个相似结论: |
|
知识梳理
直线和平面垂直
2、判定方法 (2)判定定理:如果一条直线和一个平面内两条相交直线都垂直,那么这条直线垂直于这个平面. (3)其他方法:`{:(a"//"b),(b_|_alpha):}}rArra_|_alpha` `{:(alpha"//"beta),(a_|_alpha):}}rArra_|_beta` `{:(alpha_|_beta),(alphannbeta=l),(asubalpha),(a_|_l):}}rArralpha_|_beta` 3、性质定理:`{:(a_|_alpha),(bsubalpha):}}rArra_|_b`
`{:(a_|_alpha),(b_|_alpha):}}rArra"//"b` |
|
应用举例
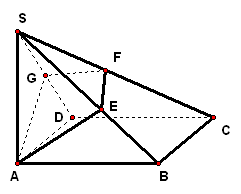
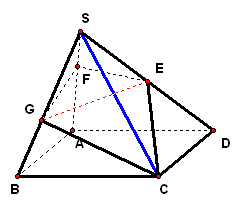
二、案例示范 1、如图,`ABCD`为正方形,`SA`垂直于`ABCD`所在的平面,过`A`且垂直于`SC`的平面分别交`SB、SC、SD`于`E、F、G` 求证:`AE_|_SB,AG_|_SD`
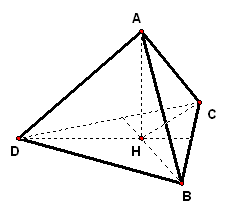
2、空间四边形`ABCD`中,`AB_|_CD,BC_|_AD,求证:AC_|_BD`
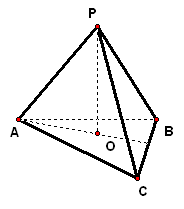
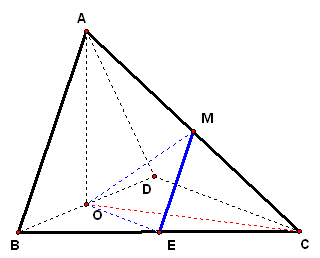
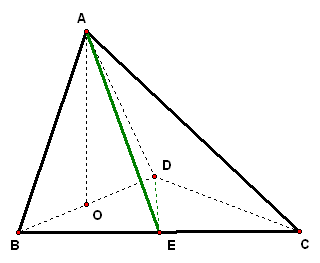
3、(06·福建)四面体`ABCD`中,`O、E`分别是`BD、BC`的中点,`CA=CB=CD=BD=2`,`AB=AD=sqrt2`
|
|
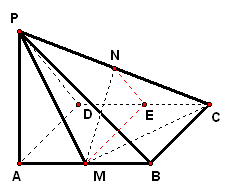
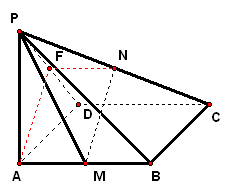
实践体验 1、已知`PA`垂直于矩形`ABCD`所在平面,`M、N`分别是`AB、PC`的中点,若`/_PDA=45°` 求证:`MN_|_平面PCD`
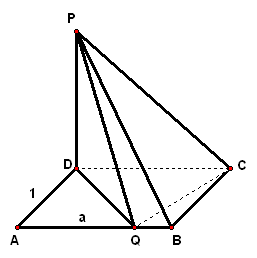
2、在矩形`ABCD`中,`AB=1`,`BC=a`,`PA_|_`平面`ABCD`,且`PA=1`,问`BC`边上是否一定存在点`Q`,使`PQ_|_QD`?为什么?
|
|
拓展探究
|
|
|
|
|
学习感悟 利用三垂线定理及其逆定理的关键是要善于从各种图形中找到“平面的垂线”、“平面的斜线”、“斜线的射影”. (2)三垂线定理及其逆定理主要用于: ①立体几何的证明问题,如线线垂直,线面垂直,面面垂直; ②立体几何的计算问题,如求空间一点到平面内某一直线的距离,求两平行直线间的距离,求两条异面直线所成角等; ③二面角问题,主要是构造二面角的平面角.(求距离及求角问题,请结合第七、第八两节内容体会) 2、直线与平面垂直是直线与平面相交的特殊情形.要弄清定义中“任意”与“无数”这两个术语内涵的差异,后者存在于前者中. (1)由线面垂直的定义可以得到两个作图的依据:过一点有且只有一条直线与一个已知平面垂直;过一点有且只有一个平面与一条已知直线垂直. (2)利用线面垂直的性质可以证明两线垂直和两线平行,也可实现线面垂直的证明,因此线面垂直是线线垂直、面面垂直关系中的枢纽. (3)判定线面垂直的方法,主要用线面垂直的定义,及两个判定定理. |