第九章  直线、平面、简单几何体(B)
 §9.2 直线与平面平行和平面与平面平行(1)

复习目标 知识梳理 应用举例 实践体验 拓展探究 基础训练 提高训练 学习感悟

    一、复习目标
    掌握直线和平面、平面和平面平行的判定定理和性质定理，并能用之解决有关问题．

    二、重点难点
    (这里输入)

    三、特别提示
    (1)在解决线面、面面平行的判定时，一般遵循从“低维”到“高维”的转化，即从“线线平行”到“线面平行”，再到“面面平行”，而在应用性质定理时，其顺序恰好相反，但也要注意，转化的方向总是视题目的具体条件而定，绝不可过于“模式化”． 

　

(2)解决有关平行问题时，应注意以下结论的应用：

①经过平面外一点有且只有一个平面和已知平面平行．

②两个平面平行，其中一个平面内的直线必平行于另一个平面．

③已知平面外的两条平行线中的一条平行于这个平面，则另一条也平行于这个平面．

④如果一条直线与两个平行平面中的一个相交，那么它与另一个也相交．

⑤一条直线垂直于两个平行平面中的一个平面，必垂直于另一个平面．

⑥夹在两个平行平面间的平行线段相等．

⑦两平行平面之间的距离处处相等．

⑧平行于同一个平面的两个平面平行．

⑨平行于同一条直线的两条直线平行．

⑩平行于同一条直线的两个平面平行或相交．

⑾平行于同一个平面的两条直线平行、相交或者异面．

　

(3)两平面平行问题常常转化为直线与平面平行，而直线与平面平行又可转化为直线与直线平行，所以注意转化思想的应用，以下为三种平行关系相互转化的示意图．

　

(4)无论是解题还是证明，一定要注意对文字语言、图形语言和符号语言进行相互转化和相互翻译，使三者之间相辅相成，相得益彰．
    知识梳理

    直线与平面平行
    1、定义：如果一条直线与一个平面没有公共点，则这条直线和这个平面平行．

    2、判定方法
    (1)用定义．

    (2)判定定理：`{:(a!subalpha),(bsubalpha),(a"//"b):}}rArra"//"alpha`

    (3)其他方法：`{:(asubbeta),(alpha"//"beta):}}rArra"//"alpha`

                `{:(alpha"//"beta),(a!subalpha),(a!subbeta),(a"//"alpha):}}rArra"//"beta`

    3、性质定理：`{:(a"//"alpha),(asubbeta),(alphannbeta=b):}}rArra"//"b`   

    应用举例
    一、应用特点
    1、直线与平面平行的判定及应用
    2、直线与平面平行的性质定理的应用
    3、利用线线平行、线面平行来计算、推理

    二、案例示范
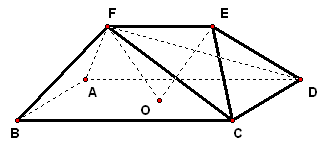
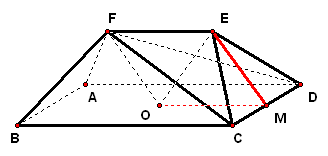
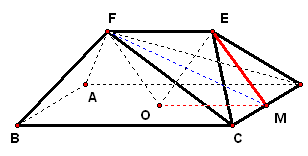
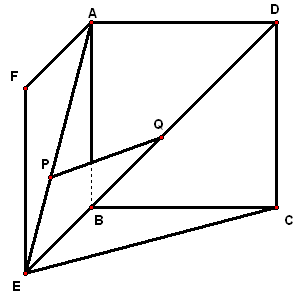
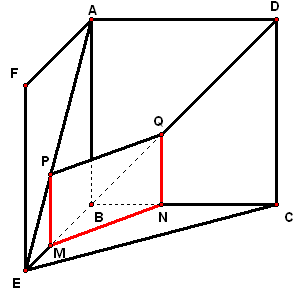
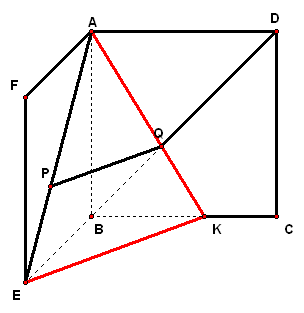
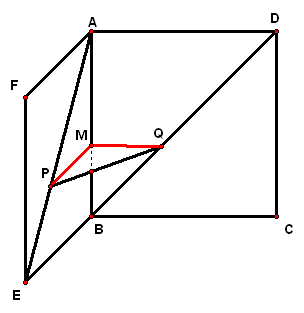
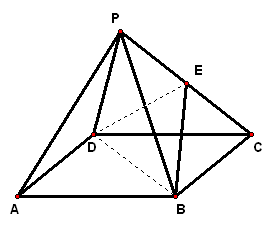
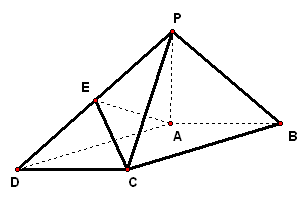
    回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范

    1、(06·天津19)如图，在五面体`ABCDEF`中，点`O`是矩形`ABCD`的对角线的交点，`△CDE`是等边三角形，棱`EF\stackrel{\////}{=}1/2BC`

    (1)证明`FO"//"`平面`CDE`

    (2)设`BC=sqrt3CD`，求证：`EO_|_`平面`CDF`

　
    提示 示范 　

   

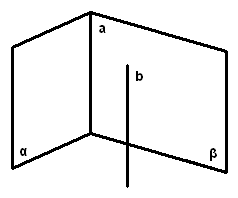
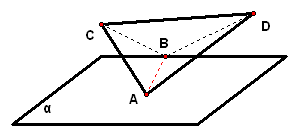
    2、如果一条直线分别与两个相交平面平行，那么这条直线与两个相交平面的交线平行．

    已知：如图，`alphannbeta=a`且`b"//"alpha`，`b"//"beta`

    求证：`b"//"a`

                                               

    提示 示范 　

   

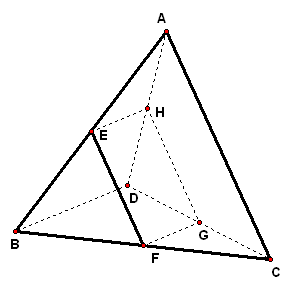
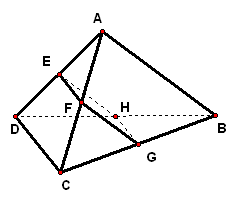
    3、空间四边形`ABCD`中，`BD_|_AC`，平行于对角线`AC、BD`的平面分别交`AB、BC、CD、DA`于点`E、F、G、H`，且`AC=a，BD=b`，求四边形`EFGH`面积的最大值．

                                              

    提示 示范 　

    实践体验
    在实践中提高能力，在体验中反思感悟，力求独立，力求提高

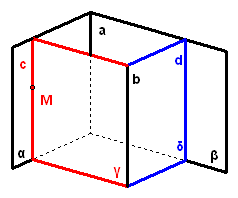
    1、如图，正方形`ABCD`与正方形`ABEF`所在平面相交于`AB`，在`AE、BD`上各有一点`P、Q`，且`AP=DQ`
    求证：`PQ"//"平面BCE`

                                              
    提示 示范 　

   

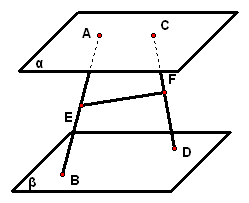
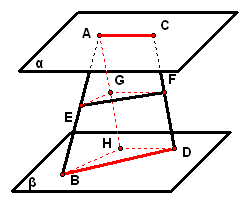
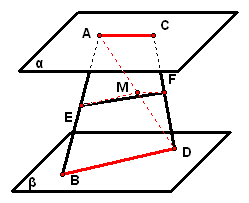
    2、如图所示，平面`alpha"//"`平面`beta`,点`Ainalpha`，点`Cinalpha`，点`Binbeta`，点`Din``beta`，点`E、F`分别在线段`AB、CD`上、且`AE:EB``=``CF:FD`
    (1)求证：`EF"//"beta`
    (2)若`E`、`F`分别是`AB`、`CD`的中点，`AC=4`，`BD=6`，且`AC`、`BD`所成的角为`60°`，求`EF`的长

                                                

    提示 示范 　

    拓展探究
    1、如图，已知正方体`ABCD-A'B'C'D'`中，面对角线`AB'、BC'`上分别有两点`E、F`且`B'E=C'F`

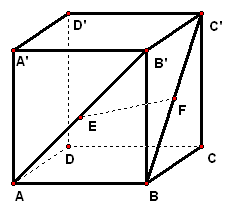
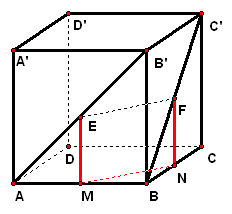
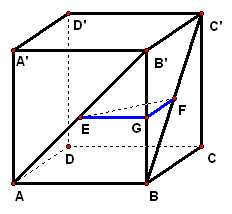
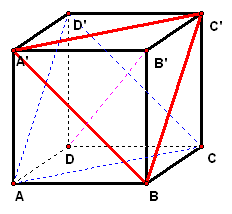
    求证：(1)`EF"//"`平面`ABCD`； (2)平面`ACD'"//"`平面`A'BC'`

                                                     

    提示 示范 　

　
    基础训练
    参考答案

 
    提高训练
    参考答案

    学习感悟
    1、直线与平面平行的判定方法有两种：

    (1)定义法，常常借助于反证法．

    (2)判定定理，判定定理与性质定理是线线平行与线面平行的转化，体现了化归与转化的数学思想．
    2、证明空间两条直线平行的两种方法：

    (1)定义．

    (2)公理4，又可利用直线和平面平行的判定与性质定理证明空间两条直线平行，判定定理与性质定理常常交替使用，即先通过线线平行推出线面平行，再通过线面平行推出新的线线平行，复杂的题目还可继续推下去．
    如下示意图可以称为平行链：

返回

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。