|
一、复习目标
2、了解空间两条直线的平行关系,直线平行关系的传递性,理解异面直线的概念.掌握异面直线的夹角、垂直的概念,了解异面直线间的距离的概念.
二、重点难点 三、特别提示 求证三点及三点以上的点共线,主要依据公理2,只要证明这些点都是两个平面的公共点,那么它们都在这两个平面的交线上;求证三条直线或三条以上的直线共点的一般方法是:首先证明两条直线交于一点,再证其余各直线都经过这点.处理好这类问题是解决高考中立体题型的基础.
(2)深刻理解有关概念,掌握异面直线的判定和计算异面直线所成角及距离的基本方法.在采用反证法判定异面直线时,可以分两种途径去论证:一是假设这两条直线共面;二是假设这两条直线平行或相交.
(3)关于距离的计算是立体几何里最常见、最基本的计算,其中异面直线的距离最为困难.按最近教育部提出调整的教学内容精神,对于异面直线的距离,只要求会计算已给出公垂线时的距离.具体解法可为两步:①证明②计算.
(4)求两条异面直线所成角的大小,一般方法是通过平行移动直线,把异面问题转化为共面问题来解决.根据空间等角定理及推论可知,异面直线所成角的大小与顶点位置无关,往往将角的顶点取在其中的一条直线上,特别地,可以取其中一条直线与另一条直线所在平面的交点或异面直线的端点. |
|
知识梳理
1、平面的基本性质 公理2:如果两个平面有一个公共点,那么它们还有其他公共点,这些公共点的集合是一条直线. 公理3:经过不在同一条直线上的三点有且只有一个平面,即不共线的三点确定一个平面. 推论1:经过一条直线和这条直线外的一点有且只有一个平面. 推论2:经过两条相交直线有且只有一个平面. 推论3:经过两条平行直线有且只有一个平面.
(2)平行直线 ②等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等. 推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.
(3)异面直线 ②两条异面直线所成的角(或夹角) 对于两条异而直线`a、b`经过空间任一点`O`作直线`a'"//"a`,`b'"//"b`,则`a'`与`b'`所成的锐角(或直角)叫做异面直线`a`与`b`所成的角(或夹角). 若两条异面直线所成的角是直角,则称这两条异面直线互相垂直. 异面直线所成的角的范围为`(0°,90°]`. ③两条异面直线的距离:和两条异面直线都垂直相交的直线叫做两条异面直线的公垂线. 两条异面直线的公垂线夹在异面直线间的部分叫做两条异面直线的距离. |
|
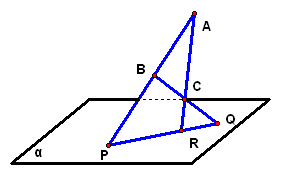
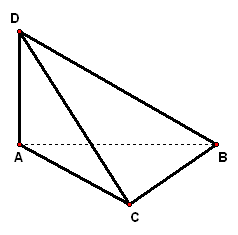
应用举例 二、案例示范 1、已知`△ABC`的三个顶点部不在平面`alpha`内,它的三边`AB、BC、AC`延长后分别交平面`alpha`于点`P、Q、R`.
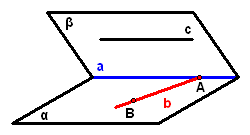
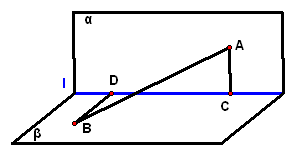
2、如图所示,已知平面`alphann`平面`beta=直线a`,直线`bsubalpha`,直线`csubbeta`,`b``nn``alpha``=A`,`c"//"alpha`,求证:`b与c是异面直线`
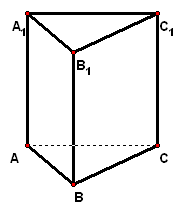
3、在直三棱柱`ABC-A_1B_1C_1`中,`/_ABC=90°`,`AB=BC=1`
|
|
实践体验 1、有空间不同的五个点
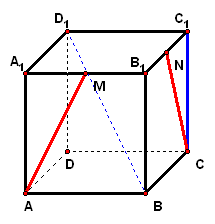
2、已知长方体`ABCD-A'B'C'D'`中,`AB=a`,`BC=b`,`A A'=c(a>b)`,求异面直线`D'B`和`AC`所成角的余弦.
|
|
拓展探究
|
|
|
|
|
学习感悟 2、异面直线是空间线线关系中重要的一种,是高考的重点,要理解它需从两个方面,一是异面直线所成的角,通常使用平移法构造三角形去解;另一个是异面直线间的距离,除了给出公垂线段的情形或使用向量法去解外,还可以考虑将线线距离转化为线面距离,最后转化为点面距离解之. |