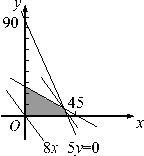|
一、复习目标 能正确画出二元一次不等式表示的平面区域;了解线性规划的意义,并能解决一些简单的实际问题. 二、重点难点 三、特别提示 |
| 知识梳理 1、二元一次不等式`Ax+By+C>0`在平面直角坐标系中表示平面区域,直线`l`应画成虚线;画不等式`Ax+By+C>=0`所表示的区域时,应把边界画成 实线. 2、若点`P(x_0,y_0)`与点`P(x_1,y_1)`在直线`l:Ax+By+C=0`的同侧,则`Ax_0+By_0+C`与`Ax_1+By_1+C`应 同号. 3、二元一次不等式组所表示的平面区域是各个不等式所表示的平面点集的交集,即各个不等式所表示的平面区域的公共部分. 4、对于变量`x、y`的约束条件,都是关于`x、y`的一次不等式,称为线性约束条件.`z=f(x,y)`是欲达到最值所涉及的变量`x、y`的解析式,叫 目标函数,当`f(x,y)`是`x、y`的一次解析式时,`z=f(x,y)`叫做线性目标函数. 5、求线性目标函数在线性约束条件下的最值问题称为线性规划问题,满足线性约束条件的解`(x,y)`称为线性规划问题的可行解,由所有解组成的集合叫 可行域,使目标函数取得最大或最小值的可行解叫做最优解. |
|
应用举例 二、案例示范 1、画出不等式组`{(x-y+5>=0),(x+y>=0),(x<=3):}`表示的平面区域。
2、设变量`x、y`满足条件`{(5y-x-5>=0),(2x+5y-20<=0),(2x-y-1>=0):}`,求`m=x+y`的最大值与最小值。
3、某厂拟生产甲、乙两种试销产品,每件销售收入分别为3千元、2千元。甲、乙产品都需要在`A,B`两种设备上加工,在每台`A,B`上加工一件甲所需工 时分为1工时、2工时,加工一件乙所需工时分别为2工时、1工时,`A,B`两种设备每月有效使用工时数为`a(400<=a<=500)`,求生产收入最大值的范围?
|
| 实践体验 (在实践中提高能力,在体验中反思感悟,力求独立,力求提高) 1、画出不等式组`{(x-2y+1>0),(x+2y+1>=0),(1<|x-1|<=3):}`表示的平面区域.
2、设`z=2y-2x+4`,式中`x、y`满足条件`{(0<=x<=1),(0<=y<=2),(2y-x>=1):}`求`z`的最大值和最小值
|
| 拓展探究 某公司用两种机器来生产某种产品,第一种机器每台3万美元及人民币50万元的维护费,第二种机器每台5万美元及人民币20万元的维护费.而第一种机器的年利润每台8万美元,第二种机器的年利润每台5万美元,但政府核准的外汇是美元135万元,并且公司的总维护费不得超过1800万元,问每种机器应该购买几台最好?
|
|
|
|
|
学习感悟
1、①设出决策变量,找出线性约束条件和线性目标函数; 2、在可行域内寻找最优整数解的方法: ①综合约束条件,观察、分析、验证即得点A最优解附近的整点; ②分析目标函数值(取整),结合约束条件确定整数解。注意在作平面区域时,`ax+by+c>0`和`ax+by+c>=0`,分别为虚线和实线。 |