第七章  直线和圆的方程
 §7.1 直线的方程

复习目标 知识梳理 应用举例 实践体验 拓展探究 基础训练 提高训练 学习感悟
    一、复习目标
    理解直线倾斜角和斜率的概念；掌握过两点的直线的斜率公式；掌握直线方程的点斜式、两点式和直线方程的一般式，并能根据条件熟练地求出直线的方程。

    二、重点难点
   

    三、特别提示
    1、斜率与倾斜角的相互转化
　　①`alpha!=`90°，k=tan`alpha`；
　　②斜率值与倾斜角值的转化；
　　③斜率范围与倾斜角范围的转化，此时要结合`y=tanx`在`[0，pi)`和`(pi/2，pi)`的变化规律，以及反三角函数的表示．
　　2、直线方程的三类、五种形式，要合理选用点斜式(含斜截式)，两点式(含截距式)，一般式．要深刻理解每种直线方程形式的适用范围，此时多涉及分类讨论的思想，如点斜式及斜截式的使用条件是直线斜率必须存在；两点式使用条件时直线既不与x轴垂直，也不与y轴垂直；截距式使用条件是两截距都存在且均不为零．
　　3、确定直线的方程有两条途径：一是用直线方程的五种形式，主要是待定系数法；二是用轨迹的定义，从直线的几何性质出发，建立方程，确定直线方程一般需要两个独立条件．
    知识梳理
    1、直线的倾斜角和斜率
    (1)以一个方程的解为坐标的点都是某条直线上的点，反过来，这条直线上的点的坐标都是这个方程的解．这时，这个方程就叫做这条直线的方程，这条直线叫做这个方程的直线．
    (2)在平面直角坐标系中，对于一条与x轴相交的直线，如果把x轴绕着交点按逆时针方向旋转到河直线重合时所转的最小正角记为`alpha`，那么`alpha`就叫做直线的倾斜角．
    规定：当直线和x轴平行或重合时，直线的倾斜角`alpha`=`0^。`．
    因此，直线的倾斜角的取值范围是`[0^。，180^。)`．
　　(3)斜率：倾斜角不是`90^。`的直线，它的斜率角的正切叫做这条直线的斜率，常用k表示，即k=tan`alpha`．倾斜角是90°的直线，斜率`k`不存在．
　　(4)斜率公式：当直线l经过两点`P_1(x_1，y_1)、P_2(x_2，y_2)`时，l的斜率`k=(y_2-y_1)/(x_2-x_1)`．
    2、直线的方向向量
    经过两点`P_1(x_1，y_1)、P_2(x_2，y_2)`的直线的方向向量为`vec(p_1p_2)`，其坐标为`(x_2-x_1，y_2-y_1)`．当斜率`k`存在时，方向向量的坐标可记为`(1，k)`．
    3、直线方程的三种形式
　　(1)点斜式：`y-y_1=k(x-x_1)`表示经过点`(x_1，y_1)`的直线．
    特例：`y=kx+b`表示过点`(0，b)`，斜率为`k`的直线，其中`b`表示直线在`y`轴上的截距，该方程叫直线方程的斜截式．
　　(2)两点式：`(y-y_1)/(y_2-y_1)=(x-x_1)/(x_2-x_1)`表示经过两点`P_1(x_1，y_1)、P_2(x_2，y_2)`的直线．
    特例：`x/a+y/b=1`(ab≠0)，其中a、b分别表示直线在x轴，y轴上的截距，该方程叫直线方程的截距式．
　　(3)一般式：`Ax+By+C=0`(其中A、B不同时为0)．
    4、直线的斜率与导数的几何意义
    函数y=f(x)在x=`x_0`处的导数即曲线y=f(x)在点`(x_0，f(x_0) )`处切线的斜率．

    应用举例
    一、应用特点
    1、求直线的方程；
    2、求直线斜率倾斜角的范围；
    3、直线方程的综合应用.

    二、案例示范
    (回味相关知识与方法，寻找解题办法，若有困难，可以参考“提示”，还有困难，可以参考“解答”或倾听老师的分析示范)

    1、求满足下列条件的直线方程：

    (1)通过点`(-2，2)`，且与两坐标轴所围成的三角形面积为1的直线l的方程：

    (2)已知直线`l_1:2x+y-6=0`和点A(1，-1)，过点`A`做直线l与已知直线`l_1`相交与B点，且`|AB|=5`，求直线`l`的方程.

    提示 示范 　

    2、已知直线l过点P(-1，2)，且与以A(-2，-3)、B(3，0)为端点的线段相交，求直线l的斜率的取值范围.
    提示 示范 　

    3、已知P(-3，4)，一直线l过P点。
    (1)若直线l在两坐标轴上截距相等，求直线l的方程；
    (2)若直线l在两坐标轴上截距之和为12，求直线l的方程；
    (3)若直线l与x轴负半轴、y轴正半轴分别交于A、B两点，试求`DeltaOAB`面积的最小值及此时直线l的方程。
    提示 示范 　

    实践体验
    (在实践中提高能力，在体验中反思感悟，力求独立，力求提高)
    1、求过点`(-2，2)`且与两坐标轴所围成的三角形面积为1的直线方程．
    提示 示范 　

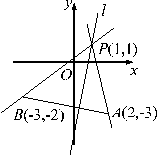
    2、若点`A(2，-3)`、`B(-3，-2)`，直线l经过点`P(1，1)`且与线段AB相交，求直线l的倾斜角及斜率的取值范围．
    提示 示范 　

    拓展探究
    若`-pi/2<alpha<0`，则直线`xtanalpha-y=0`的倾斜角为(    )
    A．`-alpha`    B．`pi/2+alpha`     C．`pi+alpha`      D．`pi/2-alpha`
    提示 示范 　

　
    基础训练
    参考答案
    提高训练
    参考答案

    学习感悟
    1、当直线与y轴垂直时，规定其倾斜角为0°y轴及与y轴平行的直线都没有斜率，但所有的直线都有倾斜角。

    2、当倾角`alpha!=90^。`时，直线的斜率`k=tanalpha=(y_2-y_1)/(x_2-x_1)`.公式中k的值与直线上两点`P_1(x_1，y_1)，P_2(x_2，y_2)`的顺序无关。

    3、直线方程的点斜式和斜截式和斜截式只能表示有斜率的直线，用来求过定点`(x_1，y_1)`的直线方程时，应注意不要忘记考虑直线`x=x_1`。

    4、斜截式是点斜式的特例、斜截距是指直线在y轴上的截距，截距不是距离，它可以取实数中的任意值。

    5、两点式不能表示与坐轴垂直的直线；截距式既不能表示与坐标轴垂直的直线，也不能表示过原点的直线。

    6、直线方程的一般式可以表示任何的一条直线；直线方程的几种特殊形式都可以化成一般式。

返回

本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。