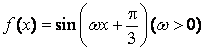 的最小正周期为
的最小正周期为福建(理)
一、选择题(每小题5分)
5、已知函数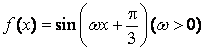 的最小正周期为
的最小正周期为![]() ,则该函数的图象( )
,则该函数的图象( )
A.关于点 对称 B.关于直线
对称 B.关于直线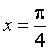 对称
对称
C.关于点 对称 D.关于直线
对称 D.关于直线![]() 对称
对称
三、解答题
17、在![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)若![]() 最大边的边长为
最大边的边长为![]() ,求最小边的边长.
,求最小边的边长.
浙江(理)
一、选择题(每小题5分)
2、若函数![]() ,
,![]() (其中
(其中![]() ,
,![]() )的最小正周期是
)的最小正周期是![]() ,
,
且![]() ,则(
)
,则(
)
A.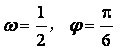 B.
B.![]()
C. D.
D.![]()
二、填空题(每小题4分)
12、已知![]() ,且
,且![]() ,则
,则![]() 的值是
.解答
的值是
.解答
三、解答题
18、已知![]() 的周长为
的周长为![]() ,且
,且![]() .
.
(I)求边![]() 的长;
的长;
(II)若![]() 的面积为
的面积为![]() ,求角
,求角![]() 的度数.
的度数.
天津(理)
一、选择题(每小题5分)
3、“![]() ”是“
”是“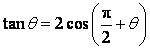 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
二、填空题(每小题4分)
15.如图,在![]() 中,
中,![]() ,
,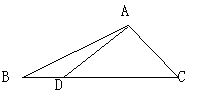
![]() 是边
是边![]() 上一点,
上一点,![]() ,则
,则![]() .
.
三、解答题
17、已知函数![]() .
.
(Ⅰ)求函数![]() 的最小正周期;
的最小正周期;
(Ⅱ)求函数![]() 在区间
在区间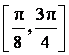 上的最小值和最大值.
上的最小值和最大值.
辽宁(理)
一、选择题(每小题5分)
5.若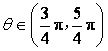 ,则复数
,则复数![]() 在复平面内所对应的点在(
)
在复平面内所对应的点在(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
三、解答题
17.(本小题满分12分)
已知函数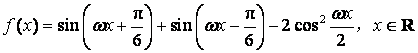 (其中
(其中![]() )
)
(I)求函数![]() 的值域;
的值域;
(II)若对任意的![]() ,函数
,函数![]() ,
,![]() 的图象与直线
的图象与直线![]() 有且仅有两个
有且仅有两个
不同的交点,试确定![]() 的值(不必证明),并求函数
的值(不必证明),并求函数![]() 的单调增区间.
的单调增区间.
重庆(理)
一、选择题(每小题5分)
5.在![]() 中,
中,![]() ,
,![]() ,
,![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题
17、设![]() .
.
(Ⅰ)求![]() 的最大值及最小正周期;
的最大值及最小正周期;
(Ⅱ)若锐角![]() 满足
满足![]() ,求
,求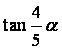 的值.
的值.
湖南(理)
二、填空题(每小题5分)
12、在![]() 中,角
中,角![]() 所对的边分别为
所对的边分别为![]() ,
,
若![]() ,b=
,b=![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
三、解答题
16、已知函数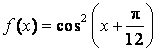 ,
,![]() .
.
(I)设![]() 是函数
是函数![]() 图象的一条对称轴,求
图象的一条对称轴,求![]() 的值.
的值.
(II)求函数![]() 的单调递增区间.
的单调递增区间.
湖北(理)
一、选择题(每小题5分)
2、将![]() 的图象按向量
的图象按向量![]() 平移,则平移后所得图象的解析式为( )
平移,则平移后所得图象的解析式为( )
A.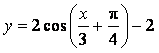 B.
B.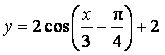
C.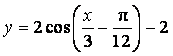 D.
D.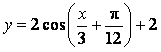
三、解答题
16、已知![]() 的面积为
的面积为![]() ,且满足
,且满足![]() ,设
,设![]() 和
和![]() 的夹角为
的夹角为![]() .
.
(I)求![]() 的取值范围;(II)求函数
的取值范围;(II)求函数![]() 的最大值与最小值.
的最大值与最小值.
江苏
一、选择题(每小题5分)
1、下列函数中,周期为![]() 的是( )
的是( )
A.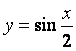 B.
B.![]() C.
C.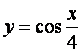 D.
D.![]()
5、函数![]() 的单调递增区间是( )
的单调递增区间是( )
A.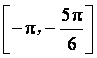 B.
B.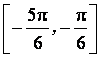 C.
C.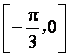 D.
D.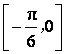
二、填空题(每小题5分)
11、若![]() ,
,![]() ,则
,则![]() _____.
_____.
15、在平面直角坐标系![]() 中,已知
中,已知![]() 的顶点
的顶点![]() 和
和![]() ,
,
顶点![]() 在椭圆
在椭圆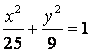 上,则
上,则![]() _____.
_____.
广东(理)
一、选择题(每小题5分)
3、若函数![]() ,则
,则![]() 是(
)
是(
)
A.最小正周期为![]() 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为![]() 的奇函数
的奇函数
C.最小正周期为![]() 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为![]() 的偶函数
的偶函数
三、解答题
16、已知![]() 顶点的直角坐标分别为
顶点的直角坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 是钝角,求
是钝角,求![]() 的取值范围.
的取值范围.
北京(理)
一、选择题(每小题5分)
1、已知![]() ,那么角
,那么角![]() 是( )
是( )
A.第一或第二象限角 B.第二或第三象限角
C.第三或第四象限角 D.第一或第四象限角
二、填空题(每小题5分)
11.在![]() 中,若
中,若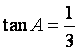 ,
,![]() ,
,![]() ,则
,则![]() .
.
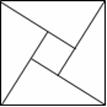
13、2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽的弦图
为基础设计的.弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方
形(如图).如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小
的锐角为![]() ,那么
,那么![]() 的值等于
.
的值等于
.
上海(理)
一、填空题(每小题4分)
6、函数 的最小正周期
的最小正周期![]()
三、解答题
17、在![]() 中,
中,![]() 分别是三个内角
分别是三个内角![]() 的对边.若
的对边.若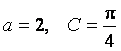 ,
,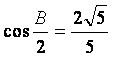 ,
,
求![]() 的面积
的面积![]() .
.
山东(理)
一、选择题(每小题5分)
(1)若![]() (i为虚数单位),则使
(i为虚数单位),则使![]() 的
的![]() 值可能是(
)
值可能是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、函数![]() 的最小正周期和最大值分别为(
)
的最小正周期和最大值分别为(
)
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
(11)在直角![]() 中,
中,![]() 是斜边
是斜边![]() 上的高,则下列等式不成立的是(
)
上的高,则下列等式不成立的是(
)
A.![]() B.
B.![]()
C.![]() D.
D.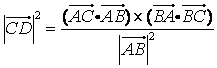
三、解答题
20、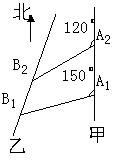 如图,甲船以每小时
如图,甲船以每小时![]() 海里的速度向正北方航行,乙船按固定方向匀速直线
海里的速度向正北方航行,乙船按固定方向匀速直线
航行,当甲船位于![]() 处时,乙船位于甲船的北偏西方向的
处时,乙船位于甲船的北偏西方向的![]() 处,此时两船相距
处,此时两船相距
![]() 海里,当甲船航行
海里,当甲船航行![]() 分钟到达
分钟到达![]() 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西![]() 方向的
方向的![]() 处,
处,
此时两船相距![]() 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?
江西(理)
一、选择题(每小题5分)
3.若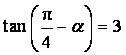 ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、若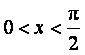 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A.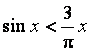 B.
B.![]() C.
C.![]() D.
D.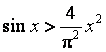
三、解答题
18、如图,函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,
,
且在该点处切线的斜率为![]() .
.
(1)求![]() 和
和![]() 的值;
的值;
(2)已知点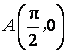 ,点
,点![]() 是该函数图象上一点,点
是该函数图象上一点,点![]()
是![]() 的中点,
的中点,
当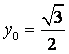 ,
,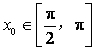 时,求
时,求![]() 的值.
的值.

陕西(理)
一、选择题(每小题5分)
4、已知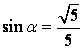 ,则
,则![]() 的值为(
)
的值为(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题
17、设函数![]() ,其中向量
,其中向量![]() ,
,![]() ,
,![]() ,
,
且![]() 的图象经过点
的图象经过点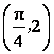 .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求函数![]() 的最小值及此时
的最小值及此时![]() 值的集合.
值的集合.
安徽(理)
一、选择题(每小题5分)
6、函数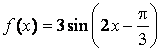 的图象为
的图象为![]() ,
,
①图象![]() 关于直线
关于直线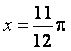 对称;
对称;
②函数![]() 在区间
在区间 内是增函数;
内是增函数;
③由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到图象
个单位长度可以得到图象![]() .
.
以上三个论断中,正确论断的个数是( )
A.0 B.1 C.2 D.3
三、解答题
16、已知![]() 为
为![]() 的最小正周期,
的最小正周期,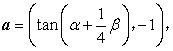
![]() ,且
,且![]()
![]() .求
.求![]() 的值.
的值.
四川(理)
一、选择题(每小题5分)
(11)如图,l1、l2、l3是同一平面内的三条平行直线,l1与l2间的距离是1,
l2与l3间的距离是2,正三角形ABC的三顶点
分别在l1、l2、l3上,
则△ABC的边长是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
二、填空题(每小题4分)
16、下面有五个命题:
①函数y=sin4x-cos4x的最小正周期是![]() .
.
②终边在y轴上的角的集合是{a|a=![]() |.
|.
③在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点.
④把函数![]()
⑤函数![]()
其中真命题的序号是 (写出所言)
三、解答题
17、已知![]() <
<![]() <
<![]() <
<![]() ,
,
(Ⅰ)求![]() 的值.
的值.
(Ⅱ)求![]() .
.
海南宁夏(理)
一、选择题(每小题5分)
1.已知命题![]() ,
,![]() ,则( )
,则( )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
3、函数 在区间
在区间 的简图是( )
的简图是( )

9、若 ,则
,则![]() 的值为( )
的值为( )
A. B.
B.![]() C.
C.![]() D.
D.![]()
三、解答题
17、如图,测量河对岸的塔高![]() 时,可以选与塔底
时,可以选与塔底![]() 在同一水平面内的两个
在同一水平面内的两个
测点![]() 与
与![]() .现测得
.现测得![]() ,并在点
,并在点![]() 测得塔顶
测得塔顶![]() 的仰角为
的仰角为![]() ,
,
求塔高![]() .
.
全国卷(Ⅰ)理
一、选择题(每小题5分)
1、![]() 是第四象限角,
是第四象限角,![]() ,则
,则![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12、函数![]() 的一个单调增区间是(
)
的一个单调增区间是(
)
A. B.
B. C.
C. D.
D.
三、解答题
17、设锐角三角形![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,
,![]() .
.
(Ⅰ)求![]() 的大小;
的大小;
(Ⅱ)求![]() 的取值范围.
的取值范围.
全国卷(Ⅱ)理
一、选择题(每小题5分)
1、![]() (
)
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、函数![]() 的一个单调增区间是(
)
的一个单调增区间是(
)
A.![]() B.
B. C.
C. D.
D.
三、解答题
17、在![]() 中,已知内角
中,已知内角 ,边
,边![]() .设内角
.设内角![]() ,周长为
,周长为![]() .
.
(1)求函数![]() 的解析式和定义域;
的解析式和定义域;
(2)求![]() 的最大值.
的最大值.