|
诱导公式应用步骤<-->正弦曲线
五点法
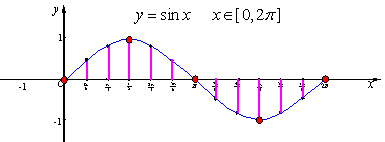
〖定义〗正弦函数的图象在[0,2π]上有五个起关键作用的点,只要描出这五个点,函数y=sinx在[0,2π]上的图象的形状就基本上确定了,我们称之为“五点法”。
这五点是: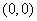 , ,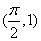 , ,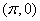 , ,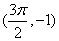 , ,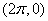 ,可分别称之为始点、最高点、拐点、最低点、终点。 ,可分别称之为始点、最高点、拐点、最低点、终点。
详解:〖概念辨析〗
1、观察正弦曲线,余弦曲线可知,在区间 上,以上五个点分别是最高点,最低点以及与x轴的交点,在确定函数的图象形状起到关键作用。 上,以上五个点分别是最高点,最低点以及与x轴的交点,在确定函数的图象形状起到关键作用。
2、在精确度要求不太高时,我们常常先描出这五个点,然后用光滑的曲线将它们连接起来,就得到在相应区间内正弦函数、余弦函数的简图,
〖相关知识〗正弦曲线
诱导公式应用步骤<-->正弦曲线
全网搜索"五点法"相关
|

