|
13.4.1 平面的基本知识<-->13.4.3 平行公理和空间等角定理
平面的性质
(1)公理1:
①叙述:如果一条直线上的两个点在一个平面内,那么这条直线上所有的点都在这个平面内。
②符号:若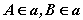 ,且 ,且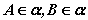 ,则 ,则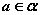 。 。
③图形;
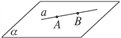
④作用:直线在平面内作图,判断或证明直线在平面内的依据。
(2)公理2:
①叙述:经过不在同一直线上的三点,有且只有一个平面。
②符号:若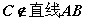 ,则 ,则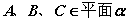 ,且 ,且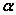 是唯一的。 是唯一的。
③图形:

④作用:确定平面的判断与作图,是判断或证明空间图形共面或异面的依据,是空间几何归面思想方法的立足点。
推论1:经过一条直线和这条直线外的一点,有且只有一个平面。
推论2:经过两条相交直线,有且只有一个平面。
推论3:经过两条平行直线,有且只有一个平面。
(3)公理3:
①叙述:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线。此时,就说两平面相交,交线就是公共点的集合。
②符号:若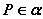 , ,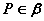 ,则 ,则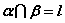 ,且 ,且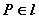 。 。
③图形:
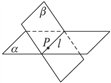
④作用:
(1)判定两个平面相交的依据,即要证明两个平面相交,必须且只需证明这两个平面有一个公共点。
(2)证明点在直线上的依据,即要证明一个点在某条直线上,可证该点是某两个平面的公共点,而该直线是这两个平面的交线。
(3)证明几个点共线的依据,即要证明几个点共线,可证这几个点都是某两个平面的公共点。
13.4.1 平面的基本知识<-->13.4.3 平行公理和空间等角定理
全网搜索"13.4.2 平面的基本性质"相关
|

