|
2022年高考数学上海春9<-->2022年高考数学上海春11
(5分)在$\Delta ABC$中,$\angle A=90^\circ$,$AB=AC=2$,点$M$为边$AB$的中点,点$P$在边$BC$上,则$\overrightarrow{MP}\cdot \overrightarrow{CP}$的最小值为 $-\dfrac{9}{8}$ .
分析:建立平面直角坐标系,利用数量积的坐标运算求出$\overrightarrow{MP}\cdot \overrightarrow{CP}=2x^{2}-3x$,再利用二次函数求最值即可.
解:建立平面直角坐标系如下,
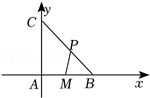
则$B(2,0)$,$C(0,2)$,$M(1,0)$,
直线$BC$的方程为$\dfrac{x}{2}+\dfrac{y}{2}=1$,即$x+y=2$,
点$P$在直线上,设$P(x,2-x)$,
$\therefore$$\overrightarrow{MP}=(x-1,2-x)$,$\overrightarrow{CP}=(x,-x)$,
$\therefore$$\overrightarrow{MP}\cdot \overrightarrow{CP}=x(x-1)-x(2-x)=2x^{2}-3x=2{(x-\dfrac{3}{4})}^{2}-\dfrac{9}{8}\geqslant -\dfrac{9}{8}$,
$\therefore$$\overrightarrow{MP}\cdot \overrightarrow{CP}$的最小值为$-\dfrac{9}{8}$.
故答案为:$-\dfrac{9}{8}$.
点评:本题考查了数量积的坐标运算,考查了二次函数求最值,属于中档题.
2022年高考数学上海春9<-->2022年高考数学上海春11
全网搜索"2022年高考数学上海春10"相关
|

