（1）因为$C_2：\rho ^2 + 2 \rho \cos \theta -3 =0$，
所以$C_2$的直角坐标方程为：$x^2+y^2+2x-3=0$。
（2）因为$C_2：x^2+y^2+2x-3=0$，即$C_2：(x+1)^2+y^2=4$，
所以$C_2$是以$(-1,0)$为圆心，$2$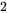
为半径的圆。
又因为$C_1：y=k|x|+2$是关于$y$轴对称的曲线，
且$C_1：y=\begin{cases}kx+2&,x \geqslant 0\\-kx+2&,x<0\end{cases}$，
显然，若$k=0$时，$C_1$与$C_2$相切，此时只有一个交点；
若$k>0$时，$C_1$与$C_2$无交点。
若$C_1$与$C_2$有且仅有三个公共点，
则必须满足$k<0$且$y=kx+2(x>0)$与$C_2$相切，
所以圆心到射线的距离为$d$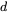
，则$d=\dfrac{|2-k|}{\sqrt{1+k^2}}=2$，
所以$k=0$或$k=-\dfrac{4}{3}$，
因为$k<0$，所以$k=-\dfrac{4}{3}$，
所以$C_1：y=k=-\dfrac{4}{3}|x|+2$。
