本题主要考查点、直线、平面的位置关系,空间直角坐标系。
(1)过点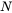 作底面垂线,再由已知条件中四棱锥的高与底面垂直,从而得到一组平行线,再利用过点
作底面垂线,再由已知条件中四棱锥的高与底面垂直,从而得到一组平行线,再利用过点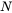 所作垂线垂足作侧边平行线来构造另外一组平行线,使得存在两组相交直线相互平行,即可证得相交直线构成的平面平行,进而得出其中一面上的任一直线与另一平面平行,证毕。
所作垂线垂足作侧边平行线来构造另外一组平行线,使得存在两组相交直线相互平行,即可证得相交直线构成的平面平行,进而得出其中一面上的任一直线与另一平面平行,证毕。
(2)以体高在底面的垂足为原点建立空间直角坐标系,利用已知中已经给出的各边数量关系,表示出面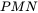 的法向量和
的法向量和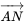 的坐标,从而求出直线方向向量与平面法向量夹角的余弦值,再通过法向量方向的判断得出直线与平面的夹角正弦值。
的坐标,从而求出直线方向向量与平面法向量夹角的余弦值,再通过法向量方向的判断得出直线与平面的夹角正弦值。

