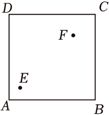
（5分）正方形草地$ABCD$边长1.2，$E$到$AB$，$AD$距离为0.2，$F$到$BC$，$CD$距离为0.4，有个圆形通道经过$E$，$F$，且与$AD$只有一个交点，求圆形通道的周长____．（精确到$0.01)$

答案：2.73．
分析：先确定圆的圆心坐标和半径，从而得出结论．
解：以$A$为原点，线段$AB$所在直线为$x$轴，$AD$所在直线为$y$轴，建立直角坐标系，
易知$E(0.2,0.2)$，$F(0.8,0.8)$．
不妨设$EF$中点为$M(0.5,0.5)$直线$EF$中垂线所在直线方程为$y-0.5=-(x-0.5)$，
化简得$y=-x+1$．
所以可设圆心为$(a,-a+1)$，半径为$a$，且经过$E$，$F$点，
即$(a-0.2)^{2}+(-a+1-0.2)^{2}=a^{2}$，
化简得$a^{2}-2a+0.68=0$，求得$a=\dfrac{2\pm \sqrt{1.28}}{2}=1\pm \sqrt{0.32}=1\pm \dfrac{4\sqrt{2}}{10}$．
结合题意可得，$a=1-\dfrac{4\sqrt{2}}{10}=0.434$．
故有圆的周长$C=2\pi a=2.725\approx 2.73$．
点评：本题主要考查直线和圆相交的性质，圆的标准方程，属于中档题．