（14分）为了解某地初中学生体育锻炼时长与学业成绩的关系，从该地区29000名学生中抽取580人，得到日均体育锻炼时长与学业成绩的数据如下表所示：
 
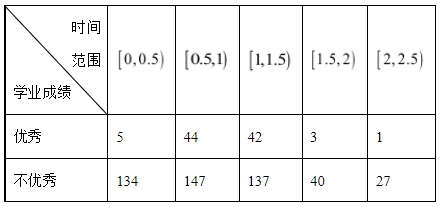
（1）该地区29000名学生中体育锻炼时长不少于1小时的人数约为多少？
（2）估计该地区初中学生日均体育锻炼的时长（精确到$0.1)$．
（3）是否有$95%$的把握认为学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关？
答案：（1）12500人；
（2）$0.9h$；
（3）学业成绩与锻炼时长不小于1小时且小于2两小时有关
分析：（1）由已知结合频率与概率关系即可求解；
（2）先求出样本平均数，然后用样本平均数估计总体平均数即可；
（3）结合独立性检验即可判断．
解：（1）580人中体育锻炼时长大于1小时人数占比$P=\dfrac{42+3+1+137+40+27}{580}=\dfrac{25}{58}$，
该地区29000名初中学生中体育锻炼时长大于1小时的人数约为$29000\times \dfrac{25}{58}=12500$；
（2）该地区初中学生锻炼平均时长约为
$\dfrac{1}{580}\times [\dfrac{1}{2}\times 0.5\times (5+134)+\dfrac{1+0.5}{2}\times (4+147)+\dfrac{1+1.5}{2}\times (42+137)+\dfrac{1.5+2}{2}\times (3+40)+\dfrac{2+2.5}{2}\times (1+27)]$
$=\dfrac{27}{29}\approx 0.9h$；
（3）由题意可得$2\times 2$列联表，

	$[1$，$2)$	其他	总数
优秀	45	50	95
不优秀	177	308	485

①提出零假设$H_{0}$：成绩优秀与日均体育锻炼时长不小于1小时且小于2小时无关，
②确定显著性水平$\alpha =0.05$，$P(x^{2}\geqslant 3.841)\approx 0.05$，
③$\chi ^2=\dfrac{580\times (45\times 308-177\times 50)^{2}}{(45+50)\times (177+308)\times (45+177)\times (50+308)}\approx 3.976 > 3.841$，
④否定零假设，即学业成绩优秀与日均体育锻炼时长不小于1小时且小于2小时有关．
点评：本题主要考查了用样本估计总体，由频率分布表求平均数及独立性检验的应用，属于中档题．