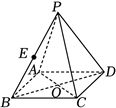
（14分）如图为正四棱锥$P-ABCD$，$O$为底面$ABCD$的中心．
（1）若$AP=5$，$AD=3\sqrt{2}$，求$\Delta POA$绕$PO$旋转一周形成的几何体的体积；
（2）若$AP=AD$，$E$为$PB$的中点，求直线$BD$与平面$AEC$所成角的大小．


答案：（1）$12\pi$；
（2）$\dfrac{\pi }{4}$．
分析：（1）根据已知条件，先求出$PO$，再结合棱锥的体积公式，即可求解．
（2）建立空间直角坐标系，求出平面$AEC$的法向量，再结合向量的夹角公式，即可求解．
解：（1）因为$P-ABCD$是正四棱锥，
所以底面$ABCD$是正方形，且$OP\bot$底面$ABCD$，
因为$AD=3\sqrt{2}$，
所以$AO=OD=OB=OC=3$，
因为$AP=5$，
所以$PO=\sqrt{AP^2-AO^2}=4$，
所以$\Delta POA$绕$OP$旋转一周形成的几何体是以3为底面半径，4为高的圆锥，
所以${{V}_{}}=\dfrac{1}{3}Sh=\dfrac{1}{3}\pi \times {{3}^{2}}\times 4=12\pi $；
（2）如图建立空间直角坐标系，

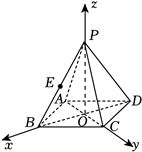
因为$AP=AD$，由题知$P-ABCD$是正四棱锥，所以该四棱锥各棱长相等，
设$AB=\sqrt{2}a$，
则$AO=OD=OB=OC=a$，$PO=\sqrt{AP^2-AO^2}=a$，
则$O(0，0，0)$，$P(0，0，a)$，$A(0，-a，0)$，$B(a，0，0)$，$C(0，a，0)$，$D(-a，0，0)$，$E(\dfrac{a}{2},0,\dfrac{a}{2})$，
故$\overrightarrow{BD}=(-2a,0,0)$，$\overrightarrow{AC}=(0,2a,0)$，$\overrightarrow{AE}=(\dfrac{a}{2},a,\dfrac{a}{2})$，
设$\overrightarrow{n}=(x_1,y_1,z_1)$为平面$AEC$的法向量，
则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{AC}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{AE}=0}\end{array}\right.$，即$\left\{\begin{array}{l}{2a\cdot {y}_{1}=0}\\ {\dfrac{a}{2}\cdot {x}_{1}+a\cdot {y}_{1}+\dfrac{a}{2}\cdot {z}_{1}=0}\end{array}\right.$，令$x_{1}=1$，则$y_{1}=0$，$z_{1}=-1$，
所以$\overrightarrow{n}=(1,0-1)$，
则$\cos  \langle \overrightarrow{n},\overrightarrow{BD}\rangle =\dfrac{\overrightarrow{n}\cdot \overrightarrow{BD}}{\vert \overrightarrow{n}\vert \cdot \vert \overrightarrow{BD}\vert }=\dfrac{-2a}{\vert 2a\vert \cdot \vert \sqrt{2}\vert }=-\dfrac{\sqrt{2}}{2}$，
设直线$BD$与面$AEC$所成角为$\theta$，
因为$\sin  \theta =\vert \cos  \langle \overrightarrow{n},\overrightarrow{BD}\rangle \vert =\dfrac{\sqrt{2}}{2}$，
$\theta \in [0,\dfrac{\pi }{2}]$，
则$\theta =\dfrac{\pi }{4}$．
点评：本题主要考查棱锥体积的求解，以及空间向量的应用，属于中档题．