| 2024年高考数学上海16 |
|
2024-08-28 23:07:52 |
|
|
(5分)已知函数$f(x)$的定义域为$R$,定义集合$M=\{x_{0}\vert x_{0}\in R$,$x\in (-\infty ,x_{0})$,$f(x) < f(x_{0})\}$,在使得$M=[-1$,$1]$的所有$f(x)$中,下列成立的是( )
A.存在$f(x)$是偶函数
B.存在$f(x)$在$x=2$处取最大值
C.存在$f(x)$为严格增函数
D.存在$f(x)$在$x=-1$处取到极小值
答案:$B$
分析:根据函数的奇偶性、单调性、极值及最值的相关性质对各选项进行判定即可.
解:对于$A$,$x < x_{0}$时,$f(x) < f(x_{0})$,
当$x_{0}=1$时,$x_{0}\in [-1$,$1]$,
对于任意$x\in (-\infty ,1)$,$f(x) < f$(1)恒成立,
若$f(x)$是偶函数,此时$f$(1)$=f(-1)$,矛盾,故$A$错误;
对于$B$,若$f(x)$函数图像如下:
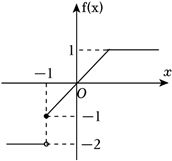
当$x < -1$时,$f(x)=-2$,$-1\leqslant x\leqslant 1$时,$f(x)\in [-1$,$1]$,当$x > 1$,$f(x)=1$,
所以存在$f(x)$在$x=2$处取最大值,故$B$正确;
对于$C$,在$x < -1$时,若函数$f(x)$严格增,
则集合$M$的取值不会是$[-1$,$1]$,而是全体定义域,故$C$错误;
对于$D$,若存在$f(x)$在$x=-1$处取到极小值,
则在$x=-1$左侧存在$x=n$,$f(n) > -1$,与集合$M$定义矛盾,故$D$错误.
故选:$B$.
点评:本题考查函数的奇偶性、单调性及最值等性质,属中档题.
|
|
http://x.91apu.com//shuxue/gkt/2024/2024sh/2024-08-28/34292.html |

