（5分）已知点$B$在点$C$正北方向，点$D$在点$C$的正东方向，$BC=CD$，存在点$A$满足$\angle BAC=16.5^\circ$，$\angle DAC=37^\circ$，则$\angle BCA=$____．（精确到0.1度）


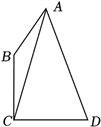
答案：$7.8^\circ$．
分析：根据已知条件，结合正弦定理，余弦定理，即可求解．
解：在$\Delta ACD$中，根据正弦定理可得$\dfrac{AC}{\sin  \angle D}=\dfrac{CD}{\sin  \angle CAD}$，
设$\angle ACB=\alpha$，则$\angle ACD=90^\circ -\alpha$，
所以$\dfrac{AC}{\sin  [180^\circ -(37^\circ +90^\circ -\alpha )]}=\dfrac{CD}{\sin  37^\circ }=\dfrac{AC}{\sin  (90^\circ -\alpha +37^\circ )}$，①
在$\Delta ABC$中，根据正弦定理可得$\dfrac{CB}{\sin  \angle BAC}=\dfrac{CA}{\sin  \angle B}$，
$\dfrac{BC}{\sin  \angle 16.5^\circ }=\dfrac{CA}{\sin  [180^\circ -(\alpha +16.5^\circ )]}=\dfrac{CA}{\sin  (\alpha +16.5^\circ )}$，②
联立①②，因为$BC=CD$，
所以$\dfrac{\sin  37^\circ }{\sin  (90^\circ -\alpha +37^\circ )}=\dfrac{\sin  16.5^\circ }{\sin  (\alpha +16.5^\circ )}$，
解得$\angle BCA=7.8^\circ$．
故答案为：$7.8^\circ$．

点评：本题主要考查解三角形，考查转化能力，属于中档题．