（15分）已知$f(x)=x+k\ln (1+x)$在$(t$，$f(t))(t > 0)$处切线为$l$．
（1）若切线$l$的斜率$k=-1$，求$f(x)$单调区间；
（2）证明：切线$l$不经过$(0,0)$；
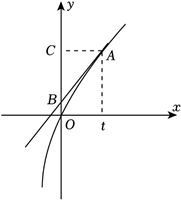
（3）已知$k=1$，$A(t$，$f(t))$，$C(0$，$f(t))$，$O(0,0)$，其中$t > 0$，切线$l$与$y$轴交于点$B$，当$2S_{\Delta ACO}=15S_{\Delta ABO}$，符合条件的$A$的个数为？
（参考数据：$1.09 < \ln 3 < 1.10$，$1.60 < \ln 5 < 1.61$，$1.94 < \ln 7 < 1.95)$
分析：（1）直接代入$k=-1$，再利用导数研究其单调性即可；
（2）写出切线方程$y-f(t)=(1+\dfrac{k}{1+t})(x-t)(t > 0)$，将$(0,0)$代入再设新函数$F(t)=\ln (1+t)-\dfrac{t}{1+t}$，利用导数研究其零点即可；
（3）分别写出面积表达式，代入$2S_{\Delta ACO}=15S_{\Delta ABO}$得到$13\ln (1+t)-2t-15\dfrac{t}{1+t}=0$，再设新函数$h(t)=13\ln (1+t)-2t-\dfrac{15t}{1+t}(t > 0)$研究其零点即可．
解：（1）$f(x)=x-\ln (1+x)$，$f'(x)=1-\dfrac{1}{1+x}=\dfrac{x}{1+x}(x > -1)$，
当$x\in (-1,0)$时，$f\prime (x) < 0$，$f(x)$在$(-1,0)$上单调递减，
当$x\in (0,+\infty )$，$f\prime (x) > 0$，$f(x)$在$(0,+\infty )$上单调递增，
则$f(x)$的单调递减区间为$(-1,0)$，单调递增区间为$(0,+\infty )$．
（2）$f'(x)=1+\dfrac{k}{1+x}$，$l$的斜率为$1+\dfrac{k}{1+t}$，
故切线方程为$y-f(t)=(1+\dfrac{k}{1+t})(x-t)(t > 0)$，
代入$(0,0)$，$-f(t)=-t(1+\dfrac{k}{1+t})$，$f(t)=t(1+\dfrac{k}{1+t})$，
$t+k\ln (1+t)=t+t\dfrac{k}{1+t}$，则$\ln (1+t)=\dfrac{t}{1+t}$，$\ln (1+t)-\dfrac{t}{1+t}=0$，
令$F(t)=\ln (1+t)-\dfrac{t}{1+t}$，
若$l$过$(0,0)$，则$F(t)$在$t\in (0,+\infty )$存在零点．
$F'(t)=\dfrac{1}{1+t}-\dfrac{1+t-t}{(1+t)^2}=\dfrac{t}{(1+t)^2} > 0$，
故$F(t)$在$(0,+\infty )$上单调递增，$F(t) > F(0)=0$，
不满足假设，故$l$不过$(0,0)$．
（3）$k=1$，$f(x)=x+\ln (1+x)$，
$f'(x)=1+\dfrac{1}{1+x}=\dfrac{x+2}{1+x} > 0$，
$S_{\Delta ACO}=\dfrac{1}{2}tf(t)$，设$l$与$y$轴交点$B$为$(0,q)$，
$t > 0$时，若$q < 0$，则此时$l$与$f(x)$必有交点，与切线定义矛盾．
由（2）知$q\ne 0$，
$\therefore q > 0$，则切线$l$的方程为$y-t-\ln (t+1)=(1+\dfrac{1}{1+t})(x-t)$，
令$x=0$，则$y=q=y=\ln (1+t)-\dfrac{t}{t+1}$，
$\because 2S_{\Delta ACO}=15S_{\Delta ABO}$，则$2tf(t)=15t[\ln (1+t)-\dfrac{t}{t+1}]$，
$\therefore$$13\ln (1+t)-2t-15\times \dfrac{t}{1+t}=0$，记$h(t)=13\ln (1+t)-2t-\dfrac{15t}{1+t}(t > 0)$，
$\therefore$满足条件的$A$有几个即$h(t)$有几个零点．
$h\prime (t)=\dfrac{13}{1+t}-2-\dfrac{15}{(t+1)^{2}}=\dfrac{13t+13-2({t}^{2}+2t+1)-15}{(t+1)^{2}}=\dfrac{2{t}^{2}+9t-4}{(t+1)^{2}}=\dfrac{(-2t+1)(t-4)}{(t+1)^{2}}$，
$t\in (0,\dfrac{1}{2})$时，$h\prime (t) < 0$，$h(t)$单调递减；
$t\in (\dfrac{1}{2},4)$时，$h\prime (t) > 0$，$h(t)$单调递增；
$t\in (4,+\infty )$时，$h\prime (t) < 0$，$h(t)$单调递减；
$\because h(0)=0$，$h(\dfrac{1}{2}) < 0$，$h$（4）$=13\ln 5-20 > 13\times 1.6-20=0.8 > 0$，
$h(24)=13\ln 25-48-\dfrac{15\times 24}{25}=26\ln 5-48-\dfrac{72}{5} < 26\times 1.61-48-\dfrac{72}{5}=-20.54 < 0$，
$\therefore$由零点存在性定理及$h(t)$的单调性，$h(t)$在$(\dfrac{1}{2},4)$上必有一个零点，在$(4,24)$上必有一个零点．
综上所述，$h(t)$有两个零点，即满足$2S_{ACO}=15S_{ABO}$的$A$有两个．

点评：本题主要考查利用导数研究函数的单调性，利用导数研究曲线上某点处的切线方程，考查运算求解能力，属于难题．