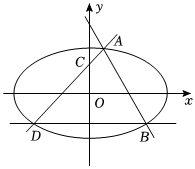
（15分）已知椭圆方程$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$，焦点和短轴端点构成边长为2的正方形，过$(0,t)(t > \sqrt{2})$的直线$l$与椭圆交于$A$，$B$，$C(0,1)$，连接$AC$交椭圆于$D$．
（1）求椭圆方程和离心率；
（2）若直线$BD$的斜率为0，求$t$．
分析：（1）根据已知条件，结合勾股定理，求出$b$，$c$，再结合椭圆的性质，即可求解；
（2）先设出直线$AB$的方程，并与椭圆的方程联立，再结合韦达定理，以及判别式，即可求解．
解：（1）椭圆方程$C:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a > b > 0)$，焦点和短轴端点构成边长为2的正方形，
则$b=c=\dfrac{2}{\sqrt{2}}=\sqrt{2}$，
故$a^{2}=b^{2}+c^{2}=2$，解得$a=\sqrt{2}$；
$a=\sqrt{b^2+c^2}=2$，
所以椭圆方程为$\dfrac{x^2}{4}+\dfrac{y^2}{2}=1$，离心率为$e=\dfrac{\sqrt{2}}{2}$；
（2）显然直线$AB$斜率存在，否则$B$，$D$重合，直线$BD$斜率不存在与题意矛盾，
同样直线$AB$斜率不为0，否则直线$AB$与椭圆无交点，矛盾，
设$AB:y=kx+t$，$(t > \sqrt{2})$，$A(x_{1}$，$y_{1})$，$B(x_{2}$，$y_{2})$，
联立$\left\{\begin{array}{l}{\;y=kx+t}\\ {\dfrac{{x}^{2}}{4}+\dfrac{{y}^{2}}{2}=1}\end{array}\right.$，化简并整理得$(1+2k^{2})x^{2}+4ktx+2t^{2}-4=0$，
由题意可知，△$=16k^{2}t^{2}-8(2k^{2}+1)(t^{2}-2)=8(4k^{2}+2-t^{2}) > 0$，即$k$，$t$应满足$4k^{2}+2-t^{2} > 0$，
由韦达定理可知，$x_1+x_2=\dfrac{-4kt}{1+2k^2}$，$x_1x_2=\dfrac{2t^2-4}{2k^2+1}$，
若直线$BD$斜率为0，由椭圆的对称性可设$D(-x_{2}$，$y_{2})$，
故$AD:y=\dfrac{y_1-y_2}{x_1+x_2}(x-x_1)+y_1$，令$x=0$，
则${y}_{C}=\dfrac{{x}_{1}{y}_{2}+{x}_{2}{y}_{1}}{{x}_{1}+{x}_{2}}=\dfrac{{x}_{1}(k{x}_{2}+t)+{x}_{2}(k{x}_{1}+t)}{{x}_{1}+{x}_{2}}=\dfrac{2k{x}_{1}{x}_{2}+t({x}_{1}+{x}_{2})}{{x}_{1}+{x}_{2}}=\dfrac{4k({t}^{2}-2)}{-4kt}+t=\dfrac{2}{t}=1$，解得$t=2$，
此时$k$满足$\left\{\begin{array}{l}{k\ne 0}\\ {4{k}^{2}+2-{t}^{2}=4{k}^{2}-2 > 0}\end{array}\right.$，解得$k > \dfrac{\sqrt{2}}{2}$或$k < -\dfrac{\sqrt{2}}{2}$，
综上所述，$t=2$满足题意，此时$k$的取值范围为$\{k\vert k < -\dfrac{\sqrt{2}}{2}$或$k > \dfrac{\sqrt{2}}{2}\}$．

点评：本题主要考查直线与椭圆的综合应用，考查转化能力，属于中档题．