（15分）已知四棱锥$P-ABCD$，$AD//BC$，$AB=BC=1$，$AD=3$，$DE=PE=2$，$E$是$AD$上一点，$PE\bot AD$．
（1）若$F$是$PE$中点，证明：$BF//$平面$PCD$．
（2）若$AB\bot$平面$PED$，求面$PAB$与面$PCD$夹角的余弦值．

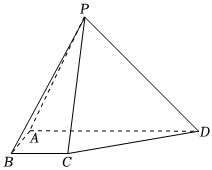
分析：（1）设$M$为$PD$的中点，连接$FM$，$CM$，证明四边形$BCMF$为平行四边形，即可得$BF//CM$，由线面平行的判定定理即可证明；
（2）易得$CE\bot$平面$PED$，以$E$为坐标原点，建立空间直角坐标系，利用向量法即可求解．
（1）证明：如图，设$M$为$PD$的中点，连接$FM$，$CM$，
因为$F$是$PE$中点，所以$FM//ED$，且$FM=\dfrac{1}{2}ED$，
因为$AD//BC$，$AB=BC=1$，$AD=3$，$DE=PE=2$，
所以四边形$ABCE$为平行四边形，$BC//ED$，且$BC=\dfrac{1}{2}ED$，
所以$FM//BC$，且$FM=BC$，
即四边形$BCMF$为平行四边形，
所以$BF//CM$，
因为$BF\not\subset$平面$PCD$，$CM\subset$平面$PCD$，
所以$BF//$平面$PCD$．
（2）解：因为$AB\bot$平面$PED$，
所以$CE\bot$平面$PED$，$EP$，$ED$，$EC$相互垂直，
以$E$为坐标原点，建立如图所示的空间直角坐标系，

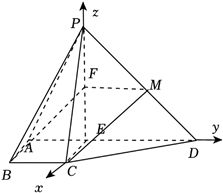
则$P(0，0，2)$，$A(0，-1，0)$，$B(1，-1，0)$，$C(1，0，0)$，$D(0，2，0)$，
所以$\overrightarrow{AB}=(1$，0，$0)$，$\overrightarrow{AP}=(0$，1，$2)$，$\overrightarrow{PC}=(1，0，-2)$，$\overrightarrow{CD}=(-1，2，0)$，
设平面$PAB$的一个法向量为$\overrightarrow{m}=(x_{1}$，$y_{1}$，$z_{1})$，
则$\left\{\begin{array}{l}{\overrightarrow{m}\cdot \overrightarrow{AB}={x}_{1}=0}\\ {\overrightarrow{m}\cdot \overrightarrow{AP}={y}_{1}+2{z}_{1}=0}\end{array}\right.$，取$z_{1}=-1$，则$\overrightarrow{m}=(0，2，-1)$，
设平面$PCD$的一个法向量为$\overrightarrow{n}=(x_{2}$，$y_{2}$，$z_{2})$，
则$\left\{\begin{array}{l}{\overrightarrow{n}\cdot \overrightarrow{PC}={x}_{2}-2{z}_{2}=0}\\ {\overrightarrow{n}\cdot \overrightarrow{CD}=-{x}_{2}+2{y}_{2}=0}\end{array}\right.$，取$z_{2}=1$，则$\overrightarrow{n}=(2，1，1)$，
设平面$PAB$与平面$PCD$夹角为$\theta$，
则$\cos  \theta =\dfrac{\overrightarrow{m}\cdot \overrightarrow{n}}{\vert \overrightarrow{m}\vert \cdot \vert \overrightarrow{n}\vert }=\dfrac{2-1}{\sqrt{5}\times \sqrt{6}}=\dfrac{1}{\sqrt{30}}=\dfrac{\sqrt{30}}{30}$．
点评：本题考查线面平行的判定定理，向量法求解二面角问题，属于中档题．