（4分）若集合$\{(x$，$y)\vert y=x+t(x^{2}-x)$，$0\leqslant t\leqslant 1$，$1\leqslant x\leqslant 2\}$表示的图形中，两点间最大距离为$d$，面积为$S$，则$($　　$)$
A．$d=3$，$S < 1$              B．$d=3$，$S > 1$              C．$d=\sqrt{10},S < 1$              D．$d=\sqrt{10},S > 1$
答案：$C$
分析：根据已知条件，作出图象，结合图象即可得出答案．
解：集合$\{y\vert y=x+t(x^{2}-x)$，$0\leqslant t\leqslant 1$，$1\leqslant x\leqslant 2\}$表示的图形如下图阴影部分所示，

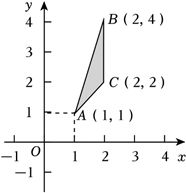
由图象可知，$d=\vert AB\vert =\sqrt{(2-1)^{2}+(4-1)^{2}}=\sqrt{10}$，$S < {S}_{\Delta ABC}=\dfrac{1}{2}\times (4-2)\times (2-1)=1$．
故选：$C$．
点评：本题考查简单的线性规划问题，涉及了二次函数的图象，考查数形结合思想，属于中档题．