（4分）已知以边长为4的正方形为底面的四棱锥，四条侧棱分别为$4,4,2\sqrt{2},2\sqrt{2}$，则该四棱锥的高为$($　　$)$
A．$\dfrac{\sqrt{2}}{2}$              B．$\dfrac{\sqrt{3}}{2}$              C．$2\sqrt{3}$              D．$\sqrt{3}$
答案：$D$
分析：根据题意分析可知平面$PEF\bot$平面$ABCD$，可知$PO\bot$平面$ABCD$，再结合等体积法，即可求解．
解：底面$ABCD$为正方形，边长为4，
当相邻的棱长相等时，
不妨设$PA=PB=AB=4$，$PC=PD=2\sqrt{2}$，
别取$AB$，$CD$的中点$E$，$F$，连接$PE$，$PF$，$EF$，
如图所示：

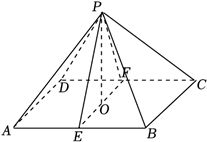
则$PE\bot AB$，$EF\bot AB$，且$PE\bigcap EF=E$，$PE$，$EF\subset$平面$PEF$，
故$AB\bot$平面$PEF$，且$AB\subset$平面$ABCD$，
所以平面$PEF\bot$平面$ABCD$，
过$P$作$EF$的垂线，垂足为$O$，即$PO\bot EF$，
由平面$PEF\bigcap$平面$ABCD=EF$，$PO\subset$平面$PEF$，
所以$PO\bot$平面$ABCD$，
由题意可得：$PE=2\sqrt{3}$，$PF=2$，$EF=4$，
则$PE^{2}+PF^{2}=EF^{2}$，即$PE\bot PF$，
则$\dfrac{1}{2}PE\cdot PF=\dfrac{1}{2}PO\cdot EF$，
故$PO=\dfrac{PE\cdot PF}{EF}=\sqrt{3}$，
所以四棱锥的高为$\sqrt{3}$，
当相对的棱长相等时，
不妨设$PA=PC=4$，$PB=PD=2\sqrt{2}$，
因为$BD=4\sqrt{2}=PB+PD$，此时不能形成三角形$PBD$，与题意不符，这样情况不存在．
故选：$D$．
点评：本题主要考查棱锥的结构特征，考查转化能力，属于难题．