（5分）若实数$x$，$y$满足约束条件$\left\{\begin{array}{l}{4x-3y-3\geqslant 0,}\\ {x-2y-2\leqslant 0,}\\ {2x+6y-9\leqslant 0,}\end{array}\right.$则$z=x-5y$的最小值为(　　)
A．5              B．$\dfrac{1}{2}$              C．$-2$              D．$-\dfrac{7}{2}$
答案：D
分析：先求出平面区域的边界点，结合$z$的几何意义检验取得最小值时点的坐标，代入即可求解．
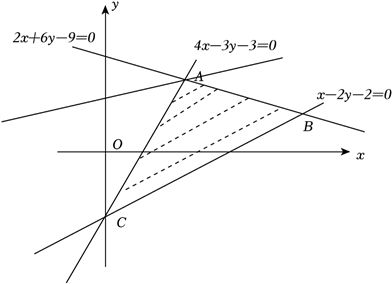
解：作出不等式组$\left\{\begin{array}{l}{4x-3y-3\geqslant 0,}\\ {x-2y-2\leqslant 0,}\\ {2x+6y-9\leqslant 0,}\end{array}\right.$所表示的平面区域，如图所示：
将约束条件两两联立可得3个交点：$C(0,-1)$，$A(\dfrac{3}{2},1)$，$B(3,\dfrac{1}{2})$，
由$z=x-5y$得$y=\dfrac{1}{5}x-\dfrac{1}{5}z$，则$-\dfrac{1}{5}z$可看作直线$y=\dfrac{1}{5}x-\dfrac{1}{5}z$在$y$轴上的截距，
经检验可知，当直线经过点$A(\dfrac{3}{2}$，$1)$时，$z$最小，代入目标函数可得：$z_{min}=-\dfrac{7}{2}$．

故选：D．
点评：本题主要考查线性规划的应用，利用$z$的几何意义是解决本题的关键，属于基础题．